题目内容
 如图所示,四边形ABCD为直角梯形,上底CD为下底AB的一半,直线l截这个梯形所得的位于此直线左方的图形面积为y,点A到直线l距离为x,则函数y=f(x)的大致图象为( )
如图所示,四边形ABCD为直角梯形,上底CD为下底AB的一半,直线l截这个梯形所得的位于此直线左方的图形面积为y,点A到直线l距离为x,则函数y=f(x)的大致图象为( )分析:当 0<x≤1时,函数y=f(x)=
hx2,图象是下凹的;当 1≤x≤2时,函数y=f(x)=hx-
h,图象是直线型,由此得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设CD=1,AB=2,设梯形的高为h,则由题意可得 tan∠DAB=
=h.
当 0<x≤1时,函数y=f(x)=
x•(x•tan∠DAB)=
•h x2,是关于x的二次函数,
它的值的增长速度逐渐加快,故图象是下凹的.
当 1≤x≤2时,函数y=f(x)=
×1×h+h×(x-1)=hx-
h,它是关于x的一次函数,故图象是直线型.
故选C.
| h |
| 1 |
当 0<x≤1时,函数y=f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
它的值的增长速度逐渐加快,故图象是下凹的.
当 1≤x≤2时,函数y=f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题主要考查函数的图象特征,函数值的增长快慢,属于基础题.

练习册系列答案
相关题目
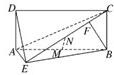 如图所示,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE.
如图所示,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE. 如图所示,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,∠ACB=120°,AB⊥PC.
如图所示,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,∠ACB=120°,AB⊥PC. 如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.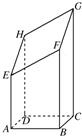 如图所示,以AB=4cm,BC=3cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5cm,BF=8cm,CG=12cm时,试回答下列问题:
如图所示,以AB=4cm,BC=3cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5cm,BF=8cm,CG=12cm时,试回答下列问题: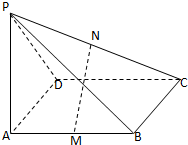 如图所示,四边形ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB,PC的中点,
如图所示,四边形ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB,PC的中点,