题目内容
当p1,p2,…,pn均为正数时,称 为p1,p2,…,pn的“均倒数”.已知数列{an}的各项均为正数,且其前n项的“均倒数”为
为p1,p2,…,pn的“均倒数”.已知数列{an}的各项均为正数,且其前n项的“均倒数”为 .
.
(1)求数列{an}的通项公式;
(2)设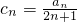 (n∈N*),试比较cn+1与cn的大小;
(n∈N*),试比较cn+1与cn的大小;
(3)设函数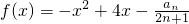 ,是否存在最大的实数λ,使当x≤λ时,对于一切正整数n,都有f(x)≤0恒成立?
,是否存在最大的实数λ,使当x≤λ时,对于一切正整数n,都有f(x)≤0恒成立?
解:(1)a1+a2+…+an-1+an=n(2n+1),a1+a2+…+an-1=(n-1)(2n-1),两式相减,得an=4n-1(n≥2).
又 ,解得 a1=3=4×1-1,
,解得 a1=3=4×1-1,
∴ …(4分)
…(4分)
(2)∵ ,
, ,
,
∴ ,即cn+1>cn.…(8分)
,即cn+1>cn.…(8分)
(3)由(2)知数列 {cn}是单调递增数列,c1=1是其最小项,即cn≥c1=1.…(9分)
假设存在最大实数,使当x≤λ时,对于一切正整数n,都有 恒成立,…(11分)
恒成立,…(11分)
则 (n∈N*).
(n∈N*).
只需-x2+4x≤c1=1,即x2-4x+1≥0,解之得 或
或  .
.
于是,可取 …(14分)
…(14分)
分析:(1)利用a1+a2+…+an-1+an=n(2n+1),再写一式,两式相减,即可得到数列{an}的通项公式;
(2)利用作差法,即可得到cn+1与cn的大小;
(3)由(2)知数列 {cn}是单调递增数列,c1=1是其的最小项.假设存在最大实数,使当x≤λ时,对于一切正整数n,都有 恒成立,即
恒成立,即 (n∈N*),利用右边的最小值,建立不等式,即可得到结论.
(n∈N*),利用右边的最小值,建立不等式,即可得到结论.
点评:本题考查数列的通项,考查大小比较,考查解不等式,确定数列的通项与单调性是关键.
又
 ,解得 a1=3=4×1-1,
,解得 a1=3=4×1-1,∴
 …(4分)
…(4分)(2)∵
 ,
, ,
,∴
 ,即cn+1>cn.…(8分)
,即cn+1>cn.…(8分)(3)由(2)知数列 {cn}是单调递增数列,c1=1是其最小项,即cn≥c1=1.…(9分)
假设存在最大实数,使当x≤λ时,对于一切正整数n,都有
 恒成立,…(11分)
恒成立,…(11分)则
 (n∈N*).
(n∈N*).只需-x2+4x≤c1=1,即x2-4x+1≥0,解之得
 或
或  .
.于是,可取
 …(14分)
…(14分)分析:(1)利用a1+a2+…+an-1+an=n(2n+1),再写一式,两式相减,即可得到数列{an}的通项公式;
(2)利用作差法,即可得到cn+1与cn的大小;
(3)由(2)知数列 {cn}是单调递增数列,c1=1是其的最小项.假设存在最大实数,使当x≤λ时,对于一切正整数n,都有
 恒成立,即
恒成立,即 (n∈N*),利用右边的最小值,建立不等式,即可得到结论.
(n∈N*),利用右边的最小值,建立不等式,即可得到结论.点评:本题考查数列的通项,考查大小比较,考查解不等式,确定数列的通项与单调性是关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
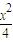 -
-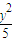 =1(x>2),O是坐标原点.
=1(x>2),O是坐标原点.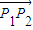 所成的比为λ(λ>0),当λ∈[
所成的比为λ(λ>0),当λ∈[ ,
, ]时,求|
]时,求|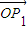 |•|
|•|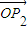 |的最值.
|的最值.