题目内容
如图,正方体ABCD—A1B1C1D1的棱长为a,过其对角线BD1的平面分别与AA1、CC1相交于点E,F,求截面四边形BED1F面积的最小值.
解:由平面与平面平行的性质定理可证BF∥D1E,BE∥D1F.
∴BED1F是平行四边形.作EH⊥BD1于H.
∵
=2·
=BD1·EH=EH·
a,
∴要求四边形BED1F面积的最小值,转化为求EH的最小值.
∵AA1∥平面BDD1B1,
∴当且仅当EH为直线AA1到平面BDD1B1的距离时,EH最小,易得EHmin=
.
∴
的最小值为
a2.
练习册系列答案
相关题目
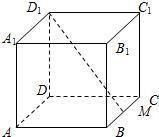如图正方体ABCD-A1B1C1D1中，M为BC中点，则直线D1M与平面ABCD所成角的正切值为
如图正方体ABCD-A1B1C1D1的棱长为1，点M是棱AA1的中点，点O是BD1的中点，求证：OM是异面直线AA1，BD1的公垂线，并求OM的长．
如图正方体ABCD-A1B1C1D1的棱长为2，则点B1到直线AC的距离是
（文）如图正方体ABCD-A1B1C1D1，在它的12条棱及12条面的对角线所在的直线中，选取若干条直线确定平面，在所有的这些平面中：
甲．如图1，平面VAD⊥平面ABCD，△VAD是等边三角形，ABCD是矩形，AB：AD=