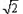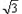题目内容
设圆C的圆心与双曲线
-y2=1(a>0)的右焦点重合,且该圆与此双曲线的渐近线相切,若直线x-
y=0被圆C截得的弦长等于1,则a的值为( )
| x2 |
| a2 |
| 3 |
分析:先利用圆与双曲线的渐近线相切得圆的半径,再利用圆C被直线x-
y=0被圆C截得的弦长等于1,根据勾股定理,确定等量关系,即可求出a.
| 3 |
解答:解:设圆心坐标为(
,0),
∵双曲线方程为
-y2=1(a>0),所以双曲线的渐近线y=
,即x-ay=0.
∵圆与双曲线的渐近线相切,
∴圆心到直线的距离等于半径,即得r=
=1,
又∵圆C被直线l:x-
y=0截得的弦长等于1,
∴圆心到直线l:x-
y=0的距离d=
=
∴a2=2
又a>0,∴a=
故选A.
| a2+1 |
∵双曲线方程为
| x2 |
| a2 |
| x |
| a |
∵圆与双曲线的渐近线相切,
∴圆心到直线的距离等于半径,即得r=
| ||
|
又∵圆C被直线l:x-
| 3 |
∴圆心到直线l:x-
| 3 |
1-
|
| ||
|
∴a2=2
又a>0,∴a=
| 2 |
故选A.
点评:本题考查直线与圆的位置关系,考查点到直线的距离公式等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查解决问题的能力和运算能力.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 -y2=1(a>0)的右焦点重合,且该圆与此双曲线的渐近线相切,若直线x-
-y2=1(a>0)的右焦点重合,且该圆与此双曲线的渐近线相切,若直线x- y=0被圆C截得的弦长等于1,则a的值为
y=0被圆C截得的弦长等于1,则a的值为
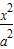 -y2=1(a>0)的右焦点重合,且该圆与此双曲线的渐近线相切,若直线x-
-y2=1(a>0)的右焦点重合,且该圆与此双曲线的渐近线相切,若直线x- y=0被圆C截得的弦长等于1,则a的值为( )
y=0被圆C截得的弦长等于1,则a的值为( )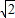
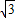
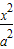 -y2=1(a>0)的右焦点重合,且该圆与此双曲线的渐近线相切,若直线x-
-y2=1(a>0)的右焦点重合,且该圆与此双曲线的渐近线相切,若直线x-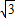 y=0被圆C截得的弦长等于1,则a的值为( )
y=0被圆C截得的弦长等于1,则a的值为( )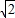
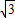
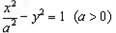 的右焦点重合,且该圆与此双曲线的渐近线相切,若直线
的右焦点重合,且该圆与此双曲线的渐近线相切,若直线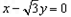 被圆C截得的弦长等于1,则a的值为
被圆C截得的弦长等于1,则a的值为