题目内容
某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,按以往比赛经验,甲胜乙的概率为| 2 | 3 |
(1)求比赛三局甲获胜的概率;
(2)求甲获胜的概率;
(3)设甲比赛的次数为X,求X的数学期望.
分析:(1)比赛三局甲获胜的概率是:P3=
(
)3=
.
(2)再求出P4和P5,甲获胜的概率是:P3+P4+P5=
.
(3)写出甲比赛次数的分布列,根据分布列求得甲比赛次数的数学期望是 EX.
| C | 3 3 |
| 2 |
| 3 |
| 8 |
| 27 |
(2)再求出P4和P5,甲获胜的概率是:P3+P4+P5=
| 64 |
| 81 |
(3)写出甲比赛次数的分布列,根据分布列求得甲比赛次数的数学期望是 EX.
解答:解:记甲n局获胜的概率为 Pn,n=3,4,5,
(1)比赛三局甲获胜的概率是:P3=
(
)3=
;
(2)比赛四局甲获胜的概率是:P4=
(
)3 (
)=
;
比赛五局甲获胜的概率是:P5=
(
)2(
)3=
;
甲获胜的概率是:P3+P4+P5=
.
(3)记乙n局获胜的概率为 Pn′,n=3,4,5.
P3′=
(
)3=
,P4′=
(
)3 (
)=
; P5′=
(
)3(
)2=
;
故甲比赛次数的分布列为:
所以甲比赛次数的数学期望是:EX=3(
+
)+4(
+
)+5(
+
)=
.
(1)比赛三局甲获胜的概率是:P3=
| C | 3 3 |
| 2 |
| 3 |
| 8 |
| 27 |
(2)比赛四局甲获胜的概率是:P4=
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
比赛五局甲获胜的概率是:P5=
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 16 |
| 81 |
甲获胜的概率是:P3+P4+P5=
| 64 |
| 81 |
(3)记乙n局获胜的概率为 Pn′,n=3,4,5.
P3′=
| C | 3 3 |
| 1 |
| 3 |
| 1 |
| 27 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 81 |
故甲比赛次数的分布列为:
| X | 3 | 4 | 5 |
| P(X) | P3+P3′ | P4+P4′ | P5+P5′ |
| 1 |
| 27 |
| 8 |
| 27 |
| 8 |
| 27 |
| 2 |
| 27 |
| 16 |
| 81 |
| 8 |
| 81 |
| 107 |
| 27 |
点评:本题考查n次独立重复试验恰好发生k次得概率,离散型随机变量的分布列和数学期望,列出离散型随机变量的分布列,是解题的难点和关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
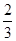 。
。