题目内容
当a>0且a≠1时,解关于x的不等式
提示:当a>1时,得2x2+x<x2+2x+2.解得-1<x<2. 当0<a<1时,得2x2+x>x2+2x+2.解得x<-1或x>2. 13.设f(x)=2x+2-3·4x,已知x2+x≤0,求f(x)的值域. 提示:∵x2+x≤0,∴-1≤x≤0.∴ 令μ=2x,则f(x)=2x+2-3·4x=-3·(2x)2+4·2x可化为y=-3μ2+4μ( 其顶点坐标为( 所以y=-3μ2+4μ(12≤μ≤1)的最大值为ymax=f(
![]() ≤2x≤1.
≤2x≤1.![]() ≤μ≤1).
≤μ≤1).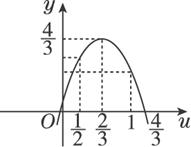
![]() ,
,![]() ),且
),且![]() ∈[
∈[![]() ,1],其图象开口向下,又在x轴上1到
,1],其图象开口向下,又在x轴上1到![]() 的距离大于
的距离大于![]() 到
到![]() 的距离,
的距离,![]() )=
)=![]() ,最小值为ymin=f(1)=1.所以f(x)=2x+2-3·4x的值域为[1,
,最小值为ymin=f(1)=1.所以f(x)=2x+2-3·4x的值域为[1,![]() ].
]. 练习册系列答案
练习册系列答案
华章教育暑假总复习学习总动员系列答案
名校课堂小练习系列答案
文轩图书假期生活指导暑系列答案
新课程暑假作业本宁波出版社系列答案
步步高高考总复习系列答案

暑假作业西南大学出版社系列答案
大赢家期末真题卷系列答案
快乐假期暑假作业新蕾出版社系列答案
步步高练加测系列答案
相关题目
 >
>