题目内容
已知函数f（x）=cos2x+
sin2x
①求f（x）的最小正周期及其单调区间；
②当x取何值时，f（x）取最大值？最大值是多少？
③在直角坐标系内，画出f（x）在一个周期内的图象．
| 3 |
①求f（x）的最小正周期及其单调区间；
②当x取何值时，f（x）取最大值？最大值是多少？
③在直角坐标系内，画出f（x）在一个周期内的图象．
f（x）=cos2x+
sin2x=2sin（2x+
），
①∵ω=2，∴f（x）的最小正周期T=
=π；
其单调增区间为2kπ-
≤2x+
≤2kπ+
，k∈Z，
即：kπ-
≤x≤kπ+
，k∈Z，
则f（x）的单调减区间是[kπ-
，kπ+
]，k∈Z；
②当2x+
=2kπ+
，k∈Z，即x=kπ+
，k∈Z时，f（x）取最大值，最大值为2；
③在直角坐标系内，画出f（x）在一个周期内的图象，如图所示；
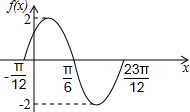
| 3 |
| π |
| 6 |
①∵ω=2，∴f（x）的最小正周期T=
| 2π |
| 2 |
其单调增区间为2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
即：kπ-
| π |
| 3 |
| π |
| 6 |
则f（x）的单调减区间是[kπ-
| π |
| 3 |
| π |
| 6 |
②当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
③在直角坐标系内，画出f（x）在一个周期内的图象，如图所示；
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
已知函数f（x）=
，则关于x的方程f2（x）+bf（x）+c=0有5个不同实数解的充要条件是（ ）
|
| A、b＜-2且c＞0 |
| B、b＞-2且c＜0 |
| C、b＜-2且c=0 |
| D、b≥-2且c=0 |
已知函数f（x）的图象如图所示，则函数的值域为（ ）