题目内容
曲线P0,P1,P2,…,已知P0所围成的图形是面积为1的等边三角形,Pk+1是对Pk进行如下操作得到的:将Pk的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(k=0,1,2,3,…),记Sn为曲线Pk所围成图形面积.
①求数列{Sn}的通项公式;
②求
Sn.

①求数列{Sn}的通项公式;
②求
| lim |
| n→∞ |

①对P0进行操作,可得P0的每条边变成P1的4条边,故P1的边数为3×4;
同样,对P1进行操作,P1的每条边变成P2的4条边,故P2的边数为3×42,从而得到Pn的边数为3×4n
已知P0的面积为S0=1,比较P1与P0,可得P1在P0的每条边上增加了一个小等边三角形,其面积为
,而P0有3条边,故S1=S0+3×
=1+
再比较P2与P1,可得P2在P1的每条边上增加了一个小等边三角形,其面积为
×
,而P1有3×4条边,故S2=S1+3×4×
=1+
+
类似地有:S3=S2+3×42×
=1+
+
+
∴Sn=1+
+
+
+…+
=1+
(
)k=
-
•(
)n(※)
下面用数学归纳法证明(※)式
当n=1时,由上面已知(※)式成立,
假设当n=k时,有Sk=
-
•(
)k,则当n=k+1时,可得第k+1次操作后,比较Pk+1与Pk,Pk+1在Pk的每条边上增加了一个小等边三角形,其面积为
,而Pk有3×4k条边.
故Sk+1=Sk+3×4k×
=
-
•(
)k+1
综上所述,对任何n∈N,(※)式成立.
②
Sn=
[
-
•(
)n]=
同样,对P1进行操作,P1的每条边变成P2的4条边,故P2的边数为3×42,从而得到Pn的边数为3×4n
已知P0的面积为S0=1,比较P1与P0,可得P1在P0的每条边上增加了一个小等边三角形,其面积为
| 1 |
| 32 |
| 1 |
| 32 |
| 1 |
| 3 |
再比较P2与P1,可得P2在P1的每条边上增加了一个小等边三角形,其面积为
| 1 |
| 32 |
| 1 |
| 32 |
| 1 |
| 34 |
| 1 |
| 3 |
| 4 |
| 33 |
类似地有:S3=S2+3×42×
| 1 |
| 36 |
| 1 |
| 3 |
| 4 |
| 33 |
| 42 |
| 35 |
∴Sn=1+
| 1 |
| 3 |
| 4 |
| 33 |
| 42 |
| 35 |
| 4n-1 |
| 32n-1 |
| 3 |
| 4 |
| n |
 |
| k=1 |
| 4 |
| 9 |
| 8 |
| 5 |
| 3 |
| 5 |
| 4 |
| 9 |
下面用数学归纳法证明(※)式
当n=1时,由上面已知(※)式成立,
假设当n=k时,有Sk=
| 8 |
| 5 |
| 3 |
| 5 |
| 4 |
| 9 |
| 1 |
| 32(k+1) |
故Sk+1=Sk+3×4k×
| 1 |
| 32(k+1) |
| 8 |
| 5 |
| 3 |
| 5 |
| 4 |
| 9 |
综上所述,对任何n∈N,(※)式成立.
②
| lim |
| n→∞ |
| lim |
| n→∞ |
| 8 |
| 5 |
| 3 |
| 5 |
| 4 |
| 9 |
| 8 |
| 5 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
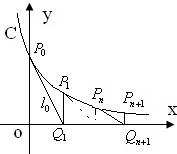 如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
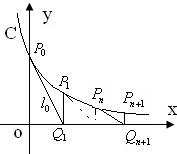 如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).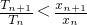 (n∈N+).
(n∈N+).