Question

（本小题满分12分）

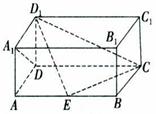
     如图，在长方体中，，，点在棱上移动。

   （I） 证明：；

   （Ⅱ）当为的中点时，求点到面的距离；

（Ⅲ）等于何值时，二面角的大小为。

Answer 1

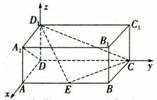
[方法一]

以点为原点，、、所在直线分别为轴，轴， 轴建立如图所示的空间直角坐标系。

由题意得 ，，，，。

（Ⅰ）设，则，，

     因为 ，

所以 ，即。                             ------------------------- 4分

（Ⅱ）由题意 ，则 ，，。

设平面的法向量为，{ ，

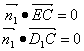
记 ，所以点到面的距离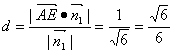。 ---------- 8分

（Ⅲ）设，则，设平面的法向量为，

{ ，

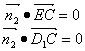
设，而平面的法向量，

由于二面角的大小为，

∴   。

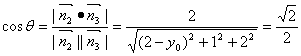
∴ 当时，二面角的大小为。              ------------------ 12分

[方法二]

（Ⅰ）连接。

在长方体中，，则四边形是正方形，又面，则。所以面，则。

（Ⅱ）连接、，则在三棱锥中有 。

由题设易证 。又面，  ∴ 为在面上的射影。

由三垂线定理，得 。设点到面的距离为，则 ，∴ ， ∴ 。

（Ⅲ）过点作于点，连接，则。

  ∴ 为二面角的平面角。设 ，则，

∴ ， 又∵ ，∴，

由题意 ，      ∴ 。

∴ 当时，二面角的大小为。