题目内容
已知函数![]()
![]()
(1)若![]() 且函数
且函数![]() 的值域为
的值域为![]() ,求
,求![]() 的表达式;
的表达式;
(2)在(1)的条件下, 当![]() 时,
时, ![]() 是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;
(3)设![]() ,
, ![]()
![]() 且
且![]() 为偶函数, 判断
为偶函数, 判断![]() +
+![]() 能否大于零?请说明理由。
能否大于零?请说明理由。
(1)![]() (2)
(2)![]() 或
或![]() (3)能
(3)能
解析:
(1) ∵![]() , ∴
, ∴![]() ①
①
又函数![]() 的值域为
的值域为![]() , 所以
, 所以![]()
且由![]() 知
知![]() 即
即![]() ②
②
由①②得 ![]()
∴![]() .
.
∴![]()
(2) 由(1)知![]()
![]() ,
,
当![]() 或
或![]() 时,
时,
 即
即![]() 或
或![]() 时, w.w.w.k.s.5 u.c.o.m
时, w.w.w.k.s.5 u.c.o.m ![]() 是具有单调性.
是具有单调性.
(3) ∵![]() 是偶函数
是偶函数
∴![]() ∴
∴![]() ,
,
∵![]() 又
又![]()
∴![]()
∴![]() +
+![]()
![]() ,
,
∴![]() +
+![]() 能大于零.
能大于零.

练习册系列答案
相关题目

 且函数
且函数 在区间
在区间 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 且函数
且函数 的值域为
的值域为 ,求
,求 的表达式;
的表达式; 为偶函数,判断
为偶函数,判断 能否大于零?并说明理由。
能否大于零?并说明理由。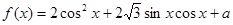 .
.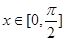 且
且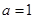 时,求
时,求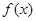 的最大值和最小值,以及取得最大值和最小值时
的最大值和最小值,以及取得最大值和最小值时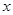 的
的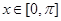 且
且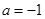 时,方程
时,方程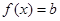 有两个不相等的实数根
有两个不相等的实数根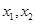 ,求
,求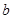 的取值
的取值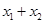 的值.
的值.