Question

数列{a_n}的前n项和公式为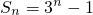，则其通项公式为________．

Answer 1

a_n=2×3^n-1．
分析：首项a₁=s₁=2，当n≥2时，a_n=s_n-s_n-1，从而得到数列的通项公式，注意验证当n=1时是否适合．
解答：由于数列{a_n}的前n项和S_n=3ⁿ-1，故首项a₁=s₁=3-1=2，
当n≥2时，a_n=s_n-s_n-1=3ⁿ-3^n-1=2×3^n-1．
经验证当n=1时，上式也适合，
故通项公式a_n=2×3^n-1．
故答案为：a_n=2×3^n-1．
点评：本题考查数列的函数特性，根据前n项和与第n项之间的关系求出通项公式，体现了分类讨论的数学思想，属于基础题．