题目内容
 某生产队要建立一个形状是直角梯形的苗圃,其两邻边借用夹角为135°的两面墙,另外两边是总长为30米的篱笆(如图,AD和DC为墙),问篱笆的两边各多长时,苗圃的面积最大?最大面积是多少?
某生产队要建立一个形状是直角梯形的苗圃,其两邻边借用夹角为135°的两面墙,另外两边是总长为30米的篱笆(如图,AD和DC为墙),问篱笆的两边各多长时,苗圃的面积最大?最大面积是多少?
分析:首先设出自变量x和函数s,设BC为x,则AB为30-x,苗圃的面积为S,由图可知苗圃是一个梯形,要表示梯形的面积必须知道梯形的上底,下底和高(过D作DE⊥AB交AB于E),梯形的上底是线段CD,下底是线段AB,高是线段DE,由题意可知四边形BCDE是一个矩形,则DE=BC=x,又因为三角形ADE为等腰直角三角形,所以AE=DE=x,则BE=CD=30-2x,根据梯形的面积公式得出S与x的二次函数关系式,求出其最大值即可.
解答:解:如图,设BC长为x,苗圃面积为S.
过D作DE⊥AB交AB于E.
由已知条件可得AB=30-x,∠DAB=45°,AE=DE=BC=x,CD=BE=AB-AE=30-2x,
∴S=
(CD+AB)•BC=
(60-3x)x=-
(x-10)2+150.由此可知,当x=10时,S取最大值.
所以,当BC=10米,AB=20米时,苗圃面积最大,这时S=150米2.
过D作DE⊥AB交AB于E.
由已知条件可得AB=30-x,∠DAB=45°,AE=DE=BC=x,CD=BE=AB-AE=30-2x,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
所以,当BC=10米,AB=20米时,苗圃面积最大,这时S=150米2.
点评:本题主要考查学生根据实际问题选择函数关系的能力,应用数学解决实际问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
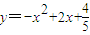 .
. 某生产队要建立一个形状是直角梯形的苗圃,其两邻边借用夹角为135°的两面墙,另外两边是总长为30米的篱笆(如图,AD和DC为墙),问篱笆的两边各多长时,苗圃的面积最大?最大面积是多少?
某生产队要建立一个形状是直角梯形的苗圃,其两邻边借用夹角为135°的两面墙,另外两边是总长为30米的篱笆(如图,AD和DC为墙),问篱笆的两边各多长时,苗圃的面积最大?最大面积是多少?