题目内容
(1)以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为θ=
(ρ∈R),它与曲线
(θ为参数)相交于两点A和B,求|AB|.
(2)在直角坐标系xOy中,直线L的参数方程为
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4cosθ.设圆C与直线L交于点A、B.若点P的坐标为(3,-2),求|PA|+|PB|及|PA|•|PB|.
| π |
| 4 |
|
(2)在直角坐标系xOy中,直线L的参数方程为
|
(1)∵ρ=
,
利用ρcosθ=x,ρsinθ=y,进行化简,
∴x-y=0,
相消去θ可得
圆的方程(x-2)2+(y-1)2=5得到圆心(2,1),半径r=
,
所以圆心(2,1)到直线的距离d=
=
,
所以|AB|=2
=3
∴线段AB的长为 3
.
(2)圆C的普通方程是(x-2)2+y2=4,
将直线l的参数方程代入并化简得t2-2
t+1=0,
由直线参数方程的几何意义得,|PA|+|PB|=2
,|PA|•|PB|=1.
| π |
| 4 |
利用ρcosθ=x,ρsinθ=y,进行化简,
∴x-y=0,
|
圆的方程(x-2)2+(y-1)2=5得到圆心(2,1),半径r=
| 5 |
所以圆心(2,1)到直线的距离d=
| 1 | ||
|
| ||
| 2 |
所以|AB|=2
| r2-d2 |
| 2 |
∴线段AB的长为 3
| 2 |
(2)圆C的普通方程是(x-2)2+y2=4,
将直线l的参数方程代入并化简得t2-2
| 5 |
由直线参数方程的几何意义得,|PA|+|PB|=2
| 5 |

练习册系列答案
相关题目
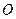 为极点,
为极点,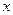 轴的正
轴的正 半轴为极
半轴为极 轴。已知点
轴。已知点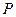 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点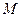 的极坐标为
的极坐标为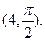 若直线
若直线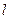 过点
过点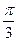 ,圆
,圆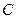 以
以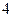 为半径。(I)求直线
为半径。(I)求直线 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于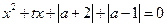 对任意
对任意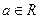 无实根,求实数
无实根,求实数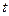 的取值范围.
的取值范围.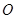 为极点,
为极点,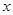 轴的正
轴的正 半轴为极
半轴为极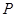 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点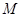 的极坐标为
的极坐标为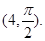 若直线
若直线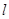 过点
过点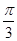 ,圆
,圆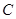 以
以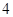 为半径。(I)求直线
为半径。(I)求直线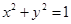 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于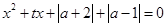 对任意
对任意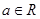 无实根,求实数
无实根,求实数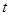 的取值范围.
的取值范围.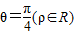 ,它与曲线
,它与曲线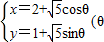 为参数)相交于两点A和B,求|AB|.
为参数)相交于两点A和B,求|AB|.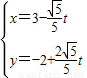 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4cosθ.设圆C与直线L交于点A、B.若点P的坐标为(3,-2),求|PA|+|PB|及|PA|•|PB|.
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4cosθ.设圆C与直线L交于点A、B.若点P的坐标为(3,-2),求|PA|+|PB|及|PA|•|PB|.