题目内容
【题目】如图1,等腰![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的四等分点,且
的四等分点,且![]() .现沿
.现沿![]() ,
,![]() ,
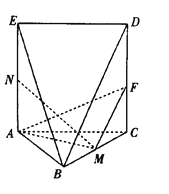
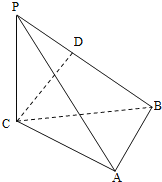
,![]() 折叠成图2所示的几何体,使
折叠成图2所示的几何体,使![]() .
.
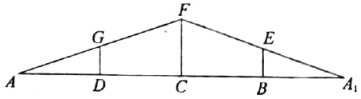
(图1)
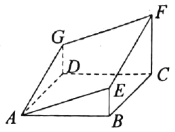
(图2)
(1)证明:![]() 平面
平面![]() ;
;
(2)求几何体![]() 的体积.
的体积.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)通过证明![]() 平面
平面![]() 、
、![]() 平面
平面![]() 来证得平面
来证得平面![]() 平面
平面![]() ,由此证得
,由此证得![]() 平面
平面![]() .
.
(2)将所求几何体![]() 分割成三棱柱和三棱锥两个部分,根据棱柱和棱锥的体积计算公式,计算出相应的体积,再相加求得几何体
分割成三棱柱和三棱锥两个部分,根据棱柱和棱锥的体积计算公式,计算出相应的体积,再相加求得几何体![]() 的体积.
的体积.
(1)由![]() ,可知四边形
,可知四边形![]() 是棱形,所以
是棱形,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)连接![]() ,
,![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
则![]() ,
,
由图1知![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
又![]() ,所以几何体
,所以几何体![]() 为直三棱柱,
为直三棱柱,![]() 平面
平面![]() .
.
由图1,直角三角形![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,
,
由![]() ,
,![]() 知三角形
知三角形![]() 为正三角形,则
为正三角形,则![]() ,
,
所以![]()
![]() .
.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目