题目内容
已知函数f(x)=ax3+bx2-2x在x=-2,x=1处取得极值.(1)求函数f(x)的解析式;
(2)求函数f(x)的单调区间.
分析:通过联立方程组求a、b得解析式;然后根据导数符号讨论单调区间.
解:(1)f′(x)=3ax2+2bx-2.
因为f(x)在x=-2,x=1处取得极值,
所以f′(-2)=0,f′(1)=0,
即![]() 解得
解得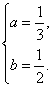
所以f(x)=![]() x3+
x3+![]() x2-2x.
x2-2x.
(2)f′(x)=x2+x-2.
由f′(x)>0,得x<-2或x>1,所以f(x)的单调增区间为(-∞,-2)和(1,+∞);
由f′(x)<0,得-2<x<1,所以f(x)的单调减区间为(-2,1).

练习册系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |