题目内容
已知a=2（cosωx，cosωx），b=（cosωx，
sinωx）（其中0＜ω＜1），函数f（x）=a•b，若直线x=
是函数f（x）图象的一条对称轴，
（1）试求ω的值；
（2）先列表再作出函数f（x）在区间[-π，π]上的图象．
| 3 |
| π |
| 3 |
（1）试求ω的值；
（2）先列表再作出函数f（x）在区间[-π，π]上的图象．
f（x）=
•
=2（cosωx，cosωx）•（cosωx，
sinωx）
=2cos2ωx+2
cosωxsinωx
=1+cos2ωx+
sin2ωx=1+2sin（2ωx+
）．
（1）∵直线x=
为对称轴，∴sin（
+
）=±1，
∴
+
=kπ+
（k∈Z）．
∴ω=
k+
，∵0＜ω＜1，
∴-
＜k＜
，∴k=0，ω=
．
（2）由（1）知，f（x）=1+2sin（x+
）．
列表：
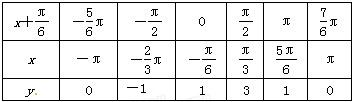
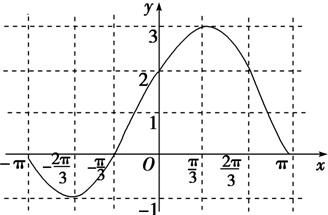
描点作图，函数f（x）在[-π，π]上的图象如图所示．
| a |
| b |
| 3 |
=2cos2ωx+2
| 3 |
=1+cos2ωx+
| 3 |
| π |
| 6 |
（1）∵直线x=
| π |
| 3 |
| 2ωπ |
| 3 |
| π |
| 6 |
∴
| 2ωπ |
| 3 |
| π |
| 6 |
| π |
| 2 |
∴ω=
| 3 |
| 2 |
| 1 |
| 2 |
∴-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
（2）由（1）知，f（x）=1+2sin（x+
| π |
| 6 |
列表：
描点作图，函数f（x）在[-π，π]上的图象如图所示．
练习册系列答案
名校课堂系列答案
相关题目
已知a=2（cosωx，cosωx），b=（cosωx，
),且a∥b,则锐角θ等于（ ）
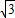sinωx）（其中0＜ω＜1），函数f（x）=a•b，若直线x=
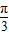是函数f（x）图象的一条对称轴，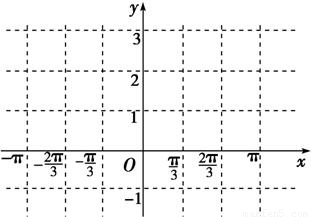
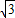sinωx）（其中0＜ω＜1），函数f（x）=a•b，若直线x=
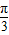是函数f（x）图象的一条对称轴，