题目内容
关于x的不等式ax＜ex在x∈（0，1）上恒成立，则a的取值范围是________．
（-∞，e]
分析：分离出参数a后，构造函数，转化为求函数的最值问题，利用导数易求函数的最值．
解答：当x∈（0，1）时，ax＜ex?a＜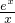
，
令f（x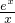）=，则问题等价于a＜f（x）min，
则f′（x）=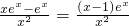
，
所以f′（x）＜0，即f（x）在（0，1）上单调递减，
所以当x∈（0，1）时，f（x）＞e，
所以a≤e，
故答案为：（-∞，e]．
点评：本题考查函数恒成立问题，考查转化思想、函数思想，解决本题的关键是对问题进行等价转化，变为函数的最值解决．
分析：分离出参数a后，构造函数，转化为求函数的最值问题，利用导数易求函数的最值．
解答：当x∈（0，1）时，ax＜ex?a＜
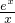，令f（x）=
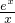，则问题等价于a＜f（x）min，则f′（x）=
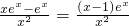，所以f′（x）＜0，即f（x）在（0，1）上单调递减，
所以当x∈（0，1）时，f（x）＞e，
所以a≤e，
故答案为：（-∞，e]．
点评：本题考查函数恒成立问题，考查转化思想、函数思想，解决本题的关键是对问题进行等价转化，变为函数的最值解决．
练习册系列答案
相关题目