题目内容
如图，在四棱锥P-ABCD中，ABCD是边长为2的菱形，∠BAD=120°，PA⊥面ABCD，且PA=11，E为BC的中点.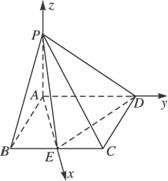
（1）（理）求二面角P-DE-A的大小；
（2）求点B到平面PDE的距离.
解析：（1）（理）∵E为中点，
∴BE=1.又AB=2，∠ABE=60°，
∴△ABE为直角三角形.
∴∠AEB=90°=∠EAD.
以A为原点，建立如图所示的坐标系.
则P（0，0，1），D（0，2，0），E（
，0，0），
∴
=(0,2,?-1),
=(
,-2,0).
设平面PDE的法向量n1=(x,y,1)，则
∴
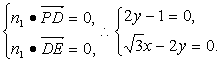
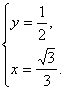
∴n1=(
,
,1).
平面ABCD的法向量n2=(0,0,1).
∴cos〈n1,n2〉=
.
∴二面角P-DE-A的大小为arccos
.
（2）B=(
,-1,0),
∴
=(-
,1,1).
∴B到面PDE的距离d=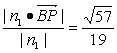
.
练习册系列答案
相关题目
如图，在四棱锥P-ABCD中，底面ABCD是矩形．已知AB=3，AD=2，PA=2，PD=2
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD为正方形，AB=4，PA=3，点A在PD上的射影为点G，点E在AB上，平面PEC⊥平面PDC．
如图，在四棱锥P-ABCD中，PA⊥底面ABCD，∠BCD=120°，BC⊥AB，CD⊥AD，BC=CD=PA=a，
如图，在四棱锥P-ABCD中，底面是边长为a的菱形，∠ABC=60°PD⊥面ABCD，PC=a，E为PB中点
（2008•武汉模拟）如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，BC∥AD，且∠BAD=90°，又PA⊥底面ABCD，BC=AB=PA=1，AD=2．