题目内容
已知函数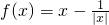
．
（I）若f（2x）=2，求x的值；
（II）若tf（t2）+mf（t）≥0对于t∈[2，4]恒成立，求实数m的取值范围．
解：（I）∵2x＞0
∴f（x）=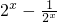
=2
∴22x-2•2x-1=0
∴
∴
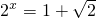
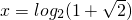
（II）∵t∈[2，4]
∴f（t）=t-
，
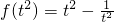
∵tf（t2）+mf（t）≥0恒成立即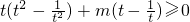
恒成立
∴（t-）（t2+1+m）≥0
∵t∈[2，4]
∴
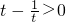
∴t2+1+m≥0
∴m≥-（t2+1）恒成立
当t∈[2，4]时，-（1+t2）∈[-17，-5]
∴m≥-5
分析：（I）由2x＞0，直接代入可求f（x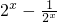）=，结合f（x）=2可求2x，进而可求x
（II）由t∈[2，4]可求f（t），f（t2），结合tf（t2）+mf（t）≥0恒成立可得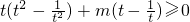恒成立，结合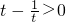整理可得m≥-（t2+1）恒成立，从而转化为求解1+t2）的最大值即可
点评：本题主要考查了指数与对数相互转化的应用及恒成立问题的求解，属于函数知识的简单应用
∴f（x）=
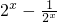=2∴22x-2•2x-1=0
∴
∴
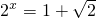
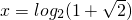
（II）∵t∈[2，4]
∴f（t）=t-
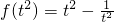
，∵tf（t2）+mf（t）≥0恒成立即
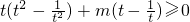恒成立∴（t-
）（t2+1+m）≥0∵t∈[2，4]
∴
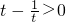
∴t2+1+m≥0
∴m≥-（t2+1）恒成立
当t∈[2，4]时，-（1+t2）∈[-17，-5]
∴m≥-5
分析：（I）由2x＞0，直接代入可求f（x）=
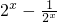，结合f（x）=2可求2x，进而可求x（II）由t∈[2，4]可求f（t），f（t2），结合tf（t2）+mf（t）≥0恒成立可得
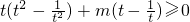恒成立，结合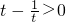整理可得m≥-（t2+1）恒成立，从而转化为求解1+t2）的最大值即可点评：本题主要考查了指数与对数相互转化的应用及恒成立问题的求解，属于函数知识的简单应用
练习册系列答案
相关题目
．
．
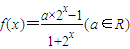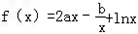处取和极值，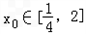
，使得不等式f（
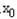）-c≤0成立，求c的最小值；
．
．
．
．
．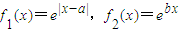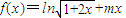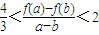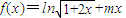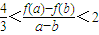