题目内容
边长为1的正三角形ABC和一半径为R的圆,若三角形和圆最多有6个公共点,则R的范围是( )
A、(1,
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|
分析:根据题意可知,当圆的半径R大于内切圆半径,小于外接圆直径时,三角形与圆最多有6个交点,所以由正三角形的边长分别求出内切圆半径和外接圆半径即可得到R的范围.
解答: 解:根据题意画出图形,如图所示:
解:根据题意画出图形,如图所示:
因为△ABC为正三角形,所以三角形的内心与外心重合,记作点O,
在直角△OBD中,∠OBD=30°,所以OD=
OB=
OA,
在直角△ABD中,由AB=1,BD=
,根据勾股定理得:
AD=
=
,
所以OD=
AD=
,2OA=
AD=
,
则R的取值范围是(
,
).
故选B
 解:根据题意画出图形,如图所示:
解:根据题意画出图形,如图所示:因为△ABC为正三角形,所以三角形的内心与外心重合,记作点O,
在直角△OBD中,∠OBD=30°,所以OD=
| 1 |
| 2 |
| 1 |
| 2 |
在直角△ABD中,由AB=1,BD=
| 1 |
| 2 |
AD=
1-(
|
| ||
| 2 |
所以OD=
| 1 |
| 3 |
| ||
| 6 |
| 4 |
| 3 |
2
| ||
| 3 |
则R的取值范围是(
| ||
| 6 |
2
| ||
| 3 |
故选B
点评:此题考查学生掌握直线与圆的位置关系的判别方法,掌握正三角形的性质,考查了数形结合的数学思想,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
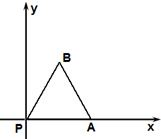 如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是
如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是 (2013•肇庆一模)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
(2013•肇庆一模)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( ) 如图所示的螺旋线是用以下方法画成的,△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别是A,B,C为圆心,AC,BA1,CA2为半径画的弧,曲线CA1A2A3称为螺旋线的第一圈;然后又以A为圆心,AA3半径画弧,如此继续下去,这样画到第n圈.设所得螺旋线CA1A2A3…A3n-2A3n-1A3n的总长度为Sn.求
如图所示的螺旋线是用以下方法画成的,△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别是A,B,C为圆心,AC,BA1,CA2为半径画的弧,曲线CA1A2A3称为螺旋线的第一圈;然后又以A为圆心,AA3半径画弧,如此继续下去,这样画到第n圈.设所得螺旋线CA1A2A3…A3n-2A3n-1A3n的总长度为Sn.求 一条曲线是用以下方法画成:△ABC是边长为1的正三角形,曲线CA1、A1A2、A2A3分别以A、B、C为圆心,AC、BA1、CA2为半径画的弧,CA1A2A3为曲线的第1圈,然后又以A为圆心,AA3为半径画弧,这样画到第n圈,则所得曲线CA1A2A3…A3n-2A3n-1A3n的总长度Sn为( )
一条曲线是用以下方法画成:△ABC是边长为1的正三角形,曲线CA1、A1A2、A2A3分别以A、B、C为圆心,AC、BA1、CA2为半径画的弧,CA1A2A3为曲线的第1圈,然后又以A为圆心,AA3为半径画弧,这样画到第n圈,则所得曲线CA1A2A3…A3n-2A3n-1A3n的总长度Sn为( )