题目内容
 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.
(I)求证:DE是⊙O的切线;
(II)若 =
= ,求
,求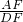 的值.
的值.
 解:(I)连接OD,可得∠ODA=∠OAD=∠DAC (2分)
解:(I)连接OD,可得∠ODA=∠OAD=∠DAC (2分)∴OD∥AE.又AE⊥DE,….(3分)
∴DE⊥OD.而OD为半径,
∴DE是⊙O的切线 (5分)
(II)由(I)得OD∥AE,
∴
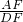 =
=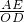 .
.又
 =
= =
= ,(8分)
,(8分)∴
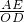 =
= ,故
,故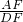 =
= (10分)
(10分)分析:(I)连接OD,根据角平分线定义和等腰三角形性质推行∠CAD=∠ODA,推出OD∥AC,根据平行线性质和切线的判定推出即可;
(II)先由(I)得OD∥AE,再结合平行线分线段成比例定理即可得到答案.
点评:考查了切线的判定定理,能够综合运用角平分线的性质、全等三角形的判定和性质以及平行线分线段成比例定理.

练习册系列答案
相关题目






 面体中有
面体中有 个面是直角三角形,则称这个
个面是直角三角形,则称这个 .那么四面体
.那么四面体 的直度为多少?说明理由;
的直度为多少?说明理由; (2)在四面体
(2)在四面体 ,设
,设 .若动点
.若动点 在四面体
在四面体 .设
.设 为动点
为动点 的函数,求
的函数,求 的正切值.
的正切值.