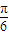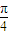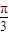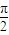题目内容
A,B,C三点在半径为1的球O面上,A,B及A,C的球面距离均为 ,且OA与平面ABC所成的角的正切值为
,且OA与平面ABC所成的角的正切值为 ,则二面角B-OA-C的大小为( )
,则二面角B-OA-C的大小为( )A.

B.

C.

D.

【答案】分析:球心O与A,B,C三点构成三棱锥O-ABC,根据线面垂直的判定定理可知AO⊥面BOC,BO⊥AO,CO⊥AO,则∠BOC为二面角B-OA-C的平面角,最后在三角形OBC中求出此角即可.
解答:解:球心O与A,B,C三点构成三棱锥O-ABC,如图所示,
已知OA=OB=OC=r=1,∠AOB=∠AOC=90°,
由此可得AO⊥面BOC,则AO⊥OE
而OA与平面ABC所成的角的正切值为 ,
,
∴OE=
则BE= ∴BC=1
∴BC=1
BO⊥AO,CO⊥AO,则∠BOC为二面角B-OA-C的平面角
∴∠BOC=
故选C
点评:本小题主要考查立体几何球面距离以及直线与平面的所成角等有关知识,同时考查空间想象能力,计算能力,属于中档题.
解答:解:球心O与A,B,C三点构成三棱锥O-ABC,如图所示,

已知OA=OB=OC=r=1,∠AOB=∠AOC=90°,
由此可得AO⊥面BOC,则AO⊥OE
而OA与平面ABC所成的角的正切值为
 ,
,∴OE=

则BE=
 ∴BC=1
∴BC=1BO⊥AO,CO⊥AO,则∠BOC为二面角B-OA-C的平面角
∴∠BOC=

故选C
点评:本小题主要考查立体几何球面距离以及直线与平面的所成角等有关知识,同时考查空间想象能力,计算能力,属于中档题.

练习册系列答案
相关题目
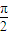 ,且OA与平面ABC所成的角的正切值为
,且OA与平面ABC所成的角的正切值为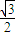 ,则二面角B-OA-C的大小为( )
,则二面角B-OA-C的大小为( )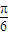

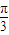

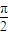 ,且OA与平面ABC所成的角的正切值为
,且OA与平面ABC所成的角的正切值为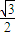 ,则二面角B-OA-C的大小为( )
,则二面角B-OA-C的大小为( )