Question

已知集合A={x|x²+4x=0}，集合B={x|x²+2（a+1）x+a²-1=0}，其中x∈R.

（1）若A∩B=B，求实数a的取值范围；

（2）若A∪B=B，求实数a的值.

Answer 1

思路解析：本题体现了分类讨论思想，要注意空集这一特殊集合.

解：（1）易知A={0，-4}，又A∩B=B，即AB.∴B=或{0}或{-4}或{0，-4}.当B=时，方程x²+2（a+1）x+a²-1=0无实数解，∴Δ=4（a+1）²-4（a²-1）＜0.解得a＜-1.当B={0}或{-4}时，方程x²+2（a+1）x+a²-1=0有两个相等实数根，∴Δ=4（a+1）²-4（a²-1）=0,得a=-1，此时B={0}，满足题意.当B={-4，0}时，方程x²+2（a+1）x+a²-1=0有两个不相等实数根-4，0，则-2（a+1）=-4+0且a²-1=0，解得a=1，此时B={x|x²+4x=0}={-4，0}，满足题意.综合以上可知a≤-1或a=1.

（2）由已知得A={0，-4}.又A∪B=B，即AB.又∵B为二次方程解集，其中最多有2个元素，∴B={0，-4}，即方程x²+2（a+1）x+a²-1=0有两根为0和-4.由韦达定理知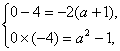

解得∴a=1.

因此，若A∪B=B，则a=1.