题目内容
已知函数f(x)=2ax3-3ax2+1, (a∈R),
(a∈R),
(Ⅰ)当a=1时,求函数y=f(x)的单调区间;
(Ⅱ)若任意给定的x0∈[0,2],在[0,2]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围。
 (a∈R),
(a∈R),(Ⅰ)当a=1时,求函数y=f(x)的单调区间;
(Ⅱ)若任意给定的x0∈[0,2],在[0,2]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围。
解:(Ⅰ)f′(x)=6x2-6x=6x(x-1),
由f′(x)>0,得x>1或x<0;由f′(x)<0,得0<x<1;
故函数f(x)的单调递增区间是(-∞,0]和[1,+∞),单调递减区间是[0,1]。
(Ⅱ)f′(x)=6ax2-6ax=6ax(x-1),
①当a=0时,显然不可能;
②当a>0时,
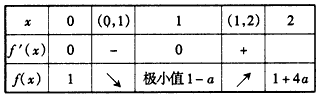
又因为当a>0时,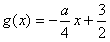 在[0,2]上是减函数,
在[0,2]上是减函数,
对任意x∈[0,2],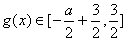 ,不合题意;
,不合题意;
③当a<0时,
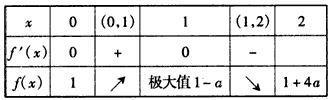
又因为当a<0时,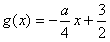 在[0,2]上是增函数,
在[0,2]上是增函数,
对任意x∈[0,2],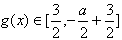 ,
,
由题意可得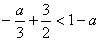 ,解得a<-1;
,解得a<-1;
综上,a的取值范围为(-∞,-1)。
由f′(x)>0,得x>1或x<0;由f′(x)<0,得0<x<1;
故函数f(x)的单调递增区间是(-∞,0]和[1,+∞),单调递减区间是[0,1]。
(Ⅱ)f′(x)=6ax2-6ax=6ax(x-1),
①当a=0时,显然不可能;
②当a>0时,

又因为当a>0时,
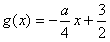 在[0,2]上是减函数,
在[0,2]上是减函数,对任意x∈[0,2],
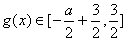 ,不合题意;
,不合题意;③当a<0时,

又因为当a<0时,
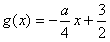 在[0,2]上是增函数,
在[0,2]上是增函数,对任意x∈[0,2],
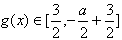 ,
,由题意可得
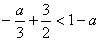 ,解得a<-1;
,解得a<-1;综上,a的取值范围为(-∞,-1)。

练习册系列答案
相关题目