题目内容
【题目】已知函数
．
（1）对于实数
，
，若
，有
，求证：方程
有两个不相等的实数根；
（2）若
，函数
，求函数
在区间
上的最大值和最小值；
（3）若存在实数
，使得对于任意实数
，都有
，求实数
的取值范围．
【答案】（1）证明见解析，（2）见解析，（3）
【解析】
（1）通过计算一元二次方程的判别式大于0，可得方程有两个不相等的实数根；
（2）化简函数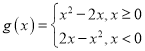
，数形结合求函数的最值；
（3）令
，
,结合二次函数的图像与性质可得结果.
（1）
，
∴
整理得：
∴
∵x1，x2∈R，x1＜x2，
∴△＞0，
故方程有两个不相等的实数根．
（2）
,
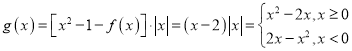作出其函数图象为：
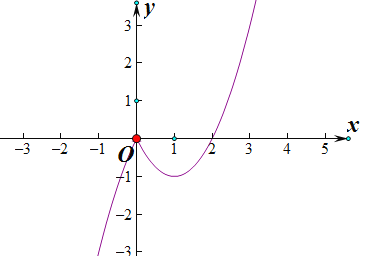
当
时，
在
上单调递增，
∴
，
；
令
，又
，∴
，
∴当
时，
，；
当
时，，；
综上：当或时，，；
当时，，；
（3）由题意可得
，
令，
∴，
∴对称轴
，
∴
，
记
，
∴
，
求根公式得：
∴
∴
即
，
故实数
的取值范围
练习册系列答案
相关题目
