题目内容
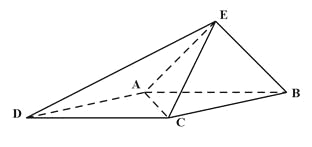
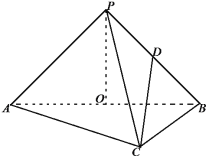
【题目】如图，在三棱锥
中，已知
，
，平面
平面
，点
分别是
的中点，
，连接
.
（1）若
，并异面直线
与所成角的余弦值的大小；
（2）若二面角
的余弦值的大小为
，求的长.
【答案】（1）
（2）
【解析】
（1）连接OC，以点O为坐标原点建立空间直角坐标系，求出
、
，利用向量法求出异面直线所成角的余弦值；
（2）设
，证得
是平面PAB的一个法向量，再求出平面PBC的一个法向量，从而可求出
，再用勾股定理求出
．
解：（1）连接OC，
∵平面PAB⊥平面ABC，PO⊥AB，∴PO⊥平面ABC，所以PO⊥OC，
∵AC=BC，点O是AB的中点，
∴OC⊥AB且
，
如图，以点O为坐标原点建立空间直角坐标系
，
．
，
．
，
，
，
，
．
从而
， 
．
∵
，
∴异面直线PA与CD所成角的余弦值的大小为；
（2）设
，则
．∵ PO⊥OC，OC⊥AB，∴OC⊥平面PAB．
从而
是平面PAB的一个法向量，
不妨设平面PBC的一个法向量为
，
∵
，
，
∴
不妨令x=1，则y=1，
，则
．
由已知，得
，化简，得．
∴
．
练习册系列答案
相关题目
