题目内容

数列{a_n}中，a₁=3，S_n为其前n项的和，满足S_n=S_n-1+a_n-1+2^n-1（n≥2），令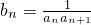 $数学公式$
（1）写出数列{a_n}的前四项，并求数列{a_n}的通项公式
（2）若f（x）=2^x-1，求和：b₁f（1）+b₂f•（2）+…+b_nf（n）
（3）设 $数学公式$ ，求证：数列{c_n}的前n项和Q_n＜2．

解：（1）数列的前四项：a₁=3，a₂=5，a₃=9，a₄=17（2分）
S_n=S_n-1+a_n-1+2^n-1（n≥2）?a_n=a_n-1+2^n-1（n≥2）（3分）
当n≥2时，a_n=（a_n-a_n-1）+•+（a₂-a₁）+a₁=2^n-1••+2^n-2++2²+2•+3=2ⁿ+1
经验证a1也符合，所以a_n=2ⁿ．+1（5分）
（2） $\text{[math]}$ = $\text{[math]}$ ，（7分）
∴b₁f（1）+b₂f（•2）+…+b_nf（n）= $\text{[math]}$ $\text{[math]}$ = $\text{[math]}$ （9分）
（3）由 $\text{[math]}$
得 $\text{[math]}$ $\text{[math]}$ （11分）
令 $\text{[math]}$
则 $\text{[math]}$ ，
相减，得 $\text{[math]}$ = $\text{[math]}$
所以 $\text{[math]}$
所以 $\text{[math]}$ （14分）
分析：（1）数列的前四项：a₁=3，a₂=5，a₃=9，a₄=17，S_n=S_n-1+a_n-1+2^n-1（n≥2）?a_n=a_n-1+2^n-1（n≥2），由此能求出a_n．
（2）由 $\text{[math]}$ = $\text{[math]}$ ，入手，能求出b₁f（1）+b₂f•（2）+…+b_nf（n）
的值．
（3）由 $\text{[math]}$ ，得 $\text{[math]}$ $\text{[math]}$ ，令 $\text{[math]}$ ，则 $\text{[math]}$ ，再由错位相减法进行求解．
点评：本题考查数列知识的综合运用，解题时要认真审题，仔细解答．