题目内容
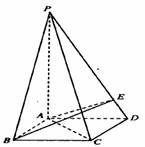
如图,四棱锥P―ABCD的底面是边长为1的正方形,PA⊥底面ABCD,PA=3,AE⊥PD,垂足为E.
(Ⅰ)求证:BE⊥PD;
(Ⅱ)求直线AC与平面EAB所成角的大小.
解法一:(Ⅰ)∵PA⊥平面ABCD,
∴PA⊥AB,
∵AB⊥AD,PA![]() AD=A
AD=A
∴PA⊥平面PAD,
又PD![]() 平面PBD,
平面PBD,
∴AB⊥PD,
又AE⊥PD,AB![]() AE=A,
AE=A,
∴PD⊥平面ABE,
∵BE![]() 平面ABE,
平面ABE,
∴BE⊥PD.
(Ⅱ)解法1:
∵CD//AB,CD![]() 平面ABE,AB
平面ABE,AB![]() 平面ABE,
平面ABE,
∴CD//平面ABE.
由(Ⅰ)知,PD⊥平面ABE,则点C到平面ABE的距离等于DE的长度.
在Rt△PAD中,PA=3,AD=1,PD=![]()
∴DE=![]()
设直线AC与平面EAB所成角的大小为![]() ,又AC=
,又AC=![]() ,
,
∴![]()
解法2:分别以AB、AD、AP为x轴、y轴、z轴建立空间直角坐标系A―xyz,则![]()
由(Ⅰ)知,PD⊥平面ABE,设直线AC与平面EAB所成角的大小为![]() ,则
,则
∴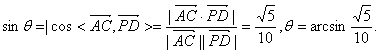

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=