题目内容
已知数列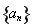 满足
满足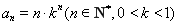 下面说法正确的是( )
下面说法正确的是( )
①当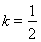 时,数列
时,数列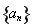 为递减数列;
为递减数列;
②当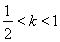 时,数列
时,数列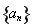 不一定有最大项;
不一定有最大项;
③当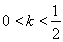 时,数列
时,数列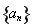 为递减数列;
为递减数列;
④当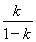 为正整数时,数列
为正整数时,数列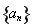 必有两项相等的最大项.
必有两项相等的最大项.
A. ①② B. ②④ C. ③④ D. ②③
【答案】
C
【解析】
试题分析: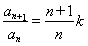 ,因为
,因为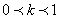 ,所以当
,所以当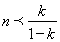 时,
时,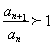 ,即
,即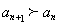 ;当
;当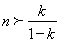 时,
时,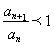 ,即
,即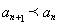 。
。
当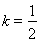 时,
时,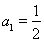 ,
,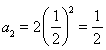 ,
,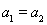 ,故数列
,故数列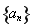 不是递减数列。故①不正确。
不是递减数列。故①不正确。
当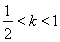 时,
时,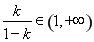 ,所以数列
,所以数列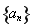 先减后增,有最大值,故②不正确。
先减后增,有最大值,故②不正确。
当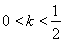 时,
时,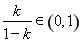 ,所以数列
,所以数列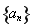 是递减数列,故③正确。
是递减数列,故③正确。
当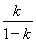 为正整数时,令
为正整数时,令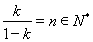 ,所以
,所以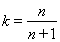
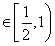 。
。
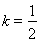 时,
时,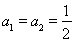 ,数列
,数列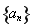 从第二项起递减,所以此时数列
从第二项起递减,所以此时数列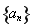 有两项相等的最大值;
有两项相等的最大值;
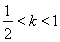 时,数列从第一项到第
时,数列从第一项到第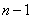 项递增,从第
项递增,从第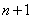 项起递减。
项起递减。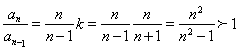 ,所以
,所以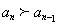 ,
,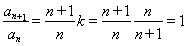 ,所以
,所以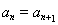 ,所以此时数列
,所以此时数列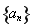 有两项相等的最大值,故④正确。
有两项相等的最大值,故④正确。
考点:数列的增减性,作商法比较大小。

练习册系列答案
相关题目