题目内容
某教育机构进行课程促销活动,促销方案是:学员每一次性购买60小时,便可以获得奖券一张,每张奖券中奖的概率为
,若中奖,则该教育机构返还学员1000元,某学员一次性购买了180h的课程,得到3张奖券,该学员购买课时的实际支出为ξ(元).(每课时100元)
(1)求ξ的所有可能取值;
(2)求ξ的分布列和数学期望Eξ.
| 1 | 5 |
(1)求ξ的所有可能取值;
(2)求ξ的分布列和数学期望Eξ.
分析:(1)设随机变量η表示中奖次数,则η的所有可能取值为0,1,2,3.当η=0时,ξ=18000;当η=1时,ξ=18000-1000=17000;…依此类推,故ξ的所有可能取值为15000,16000,17000,18000;
(2)由题意可知:η~B(3,
),则P(η=k)=
(
)k(
)3-k(k=0,1,2,3).据此即可得出ξ的分布列及其数学期望.
(2)由题意可知:η~B(3,
| 1 |
| 5 |
| C | k 3 |
| 1 |
| 5 |
| 4 |
| 5 |
解答:解:(1)设随机变量η表示中奖次数,则η的所有可能取值为0,1,2,3.当η=0时,ξ=18000;当η=1时,ξ=18000-1000=17000;当η=2时,ξ=18000-2000=16000;当η=3时,ξ=18000-3000=15000.故ξ的所有可能取值为15000,16000,17000,18000;
(2)由题意可知:η~B(3,
),则P(η=k)=
(
)k(
)3-k(k=0,1,2,3).
∴P(ξ=18000)=P(η=0)=(
)3=
;P(ξ=17000)=P(η=1)=
(
)1×(
)2=
,P(ξ=16000)=P(η=2)=
(
)2×
=
,P(ξ=15000)=P(η=3)=
×(
)3=
.
故其分布列为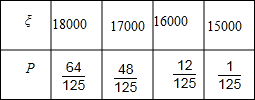
故Eξ=18000×
+17000×
+16000×
+15000×
=17400.
(2)由题意可知:η~B(3,
| 1 |
| 5 |
| C | k 3 |
| 1 |
| 5 |
| 4 |
| 5 |
∴P(ξ=18000)=P(η=0)=(
| 4 |
| 5 |
| 64 |
| 125 |
| C | 1 3 |
| 1 |
| 5 |
| 4 |
| 5 |
| 48 |
| 125 |
| C | 2 3 |
| 1 |
| 5 |
| 4 |
| 5 |
| 12 |
| 125 |
| C | 3 3 |
| 1 |
| 5 |
| 1 |
| 125 |
故其分布列为

故Eξ=18000×
| 64 |
| 125 |
| 48 |
| 125 |
| 12 |
| 125 |
| 1 |
| 125 |
点评:熟练掌握二项分布及其数学期望是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某教育机构为了研究人具有大学专科以上学历(包括大学专科)和对待教育改革态度的关系,随机抽取了392名成年人进行调查,所得数据如下表所示:
| 积极支持教育改革 | 不太赞成教育改革 | 合计 | |
| 大学专科以上学历 | 39 | 157 | 196 |
| 大学专科以下学历 | 29 | 167 | 196 |
| 合计 | 68 | 324 | 392 |
对于教育机构的研究项目,根据上述数据能得出什么结论.
