Question

已知a,b,c∈R,f(x)=ax²+bx+c,若a+c=0,f(x)在［-1,1］上最大值为2,最小值为,证明a≠0且||＜2.

Answer 1

证明:由a+c=0c=-a,故f(x)=ax²+bx+(-a).

假设a=0或||≥2.

(1)由a=0得f(x)=bx,由于b≠0,

故f(x)在［-1,1］上单调,

因此f(x)最大值为|b|,最小值为-|b|.

∴

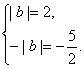
矛盾表明a≠0.

(2)由||≥2得||≥1且a≠0.

∴区间［-1,1］位于抛物线f(x)=ax²+bx-a的对称轴x=的左侧或右侧.

因此,f(x)在［-1,1］上单调,其最大值为|b|,最小值为-|b|,这是不可能的.

由此可知假设不成立,原命题成立,即a≠0且||＜2.