题目内容
已知函数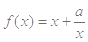 ,且
,且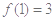 .
.
(1)求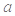 的值,并确定函数
的值,并确定函数 的定义域;
的定义域;
(2)用定义研究函数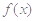 在
在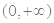 范围内的单调性;
范围内的单调性;
(3)当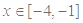 时,求出函数
时,求出函数 的取值范围.
的取值范围.
(1) ,定义域:
,定义域: ;(2)
;(2) 上是减函数,
上是减函数, 上是增函数;
上是增函数;
(3) .
.
解析试题分析:(1)直接代入列出关于 的方程即可;(2)要正确理解单调性的定义,明确用定义研究(或证明)函数的单调性的格式过程,设
的方程即可;(2)要正确理解单调性的定义,明确用定义研究(或证明)函数的单调性的格式过程,设 ,然后比较
,然后比较 和
和 的大小,通常是作差
的大小,通常是作差 (也可
(也可 ),确定差的正负;(3)由(2)中的单调性,可容易求出函数的取值范围.
),确定差的正负;(3)由(2)中的单调性,可容易求出函数的取值范围.
试题解析:(1) ,定义域:
,定义域: ; 3分
; 3分
(2)令 ,则
,则 ,
,


 6分
6分
故当 时,
时, ;当
;当 时,
时, ,
,
∴函数 在
在 上单调减,在
上单调减,在 上单调增; 8分
上单调增; 8分
(3)由(2)及函数 为奇函数知,函数
为奇函数知,函数 在
在 为增函数,在
为增函数,在 为减函数,故当
为减函数,故当 时,
时, , 10分
, 10分 ,
,
∴当 时,
时, 的取值范围是
的取值范围是 . 12
. 12
考点:(1)函数值的意义;(2)函数的单调性的定义;(3)函数的值域.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
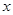 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当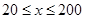 时,车流速度
时,车流速度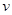 是车流密度x的一次函数.
是车流密度x的一次函数.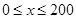 时,求函数
时,求函数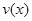 的表达式;
的表达式;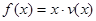 可以达到最大,并求出最大值(精确到1辆/小时)
可以达到最大,并求出最大值(精确到1辆/小时)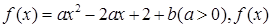 在
在 上最大值是5,最小值是2,若
上最大值是5,最小值是2,若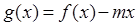 ,在
,在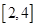 上是单调函数,求m的取值范围.
上是单调函数,求m的取值范围.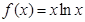 .
. 的单调区间和极值;
的单调区间和极值;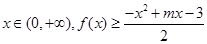 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.
 ,判断函数
,判断函数 在
在 上的单调性并用定义证明;
上的单调性并用定义证明; 的取值范围.
的取值范围.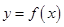 和
和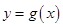 的图象关于
的图象关于 轴对称,且
轴对称,且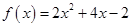 .
.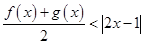 .
.
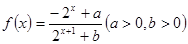 .
.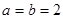 时,证明:函数
时,证明:函数 不是奇函数;
不是奇函数;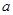 与
与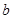 的值;
的值;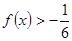 的解集.
的解集.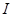 的函数
的函数 ,如果存在区间
,如果存在区间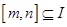 ,同时满足:
,同时满足: 在
在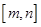 内是单调函数;②当定义域是
内是单调函数;②当定义域是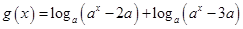 (其中
(其中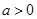 且
且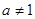 ),判断
),判断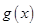 是否存在“好区间”,并
是否存在“好区间”,并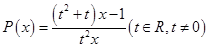 有“好区间”
有“好区间”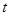 变化时,求
变化时,求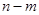 的最大值.
的最大值.