题目内容
若关于x的函数f（x）=x2-2ax+2+a有两个零点，（1）求a的取值范围．
（2）若两零点其中一个在（1，2）内，另一个在（2，3）内，求a的取值范围．
【答案】分析：（1）函数f（x）有两个零点，即方程f（x）=0有两不等实根，所以△＞0，解出即得；
（2）由条件可得不等式组得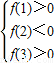
，由此可求a的范围；
解答：解：（1）因为f（x）=x2-2ax+2+a有两个零点，
所以（-2a）2-4（2+a）＞0，即a＜-1或a＞2．
所以a的取值范围为：（-∞，-1）∪（2，+∞）．
（2）由两零点一个在（1，2）内，另一个在（2，3）内，
得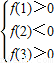
，即
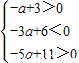，解得2＜a＜
．
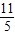所以a的取值范围为：（2，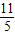
）．
点评：本题考查函数的零点与方程根的关系，函数f（x）的零点即方程f（x）=0的根，注意数形结合思想的运用．
（2）由条件可得不等式组得
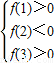，由此可求a的范围；解答：解：（1）因为f（x）=x2-2ax+2+a有两个零点，
所以（-2a）2-4（2+a）＞0，即a＜-1或a＞2．
所以a的取值范围为：（-∞，-1）∪（2，+∞）．
（2）由两零点一个在（1，2）内，另一个在（2，3）内，
得
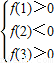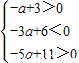，即，解得2＜a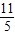＜．所以a的取值范围为：（2，
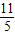）．点评：本题考查函数的零点与方程根的关系，函数f（x）的零点即方程f（x）=0的根，注意数形结合思想的运用．
练习册系列答案
相关题目
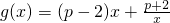，其中p≤0，若对任意的x∈[1，2]，总有2f（x）≥g（x）+4x-2x2成立，求p的取值范围．
，其中p≤0，若对任意的x∈[1，2]，总有2f（x）≥g（x）+4x-2x2成立，求p的取值范围．
，其中p≤0，若对任意的x∈[1，2]，总有2f（x）≥g（x）+4x-2x2成立，求p的取值范围．