Question

已知函数f(x)=,x∈(0,+∞),n为非零有理数,判断f(x)在(0,+∞)上是增函数还是减函数?并证明你的结论.

Answer 1

解析:要证明函数单调性可以利用作差比较f(x₁)-f(x₂)＞0的方法获得或作商比较＞1,f(x₂)≠0的方法获得.

证明:设x₁、x₂∈(0,+∞),且x₁＜x₂,则?

f(x₁)-f(x₂)==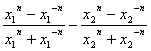

=.

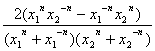
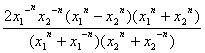∵x₁、x₂∈(0,+∞),?

∴x₁ ^-nx₂ ^-n＞0,x₁ⁿ+x₁ ^-n＞0,x₂ⁿ+x₂ ^-n＞0,x₁ⁿ+x₂ⁿ＞0.

于是.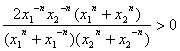

又∵0＜x₁＜x₂,为确定x₁ⁿ-x₂ⁿ的正负,需要对非零有理数n进行讨论:?

(1)n＞0时,x₁ⁿ＜x₂ⁿ,即x₁ⁿ-x₂ⁿ＜0,?

∴f(x₁)-f(x₂)＜0,即f(x₁)＜f(x₂).?

(2)n＜0时,x₁ⁿ＞x₂ⁿ,即x₁ⁿ-x₂ⁿ＞0,?

∴f(x₁)-f(x₂)＞0,即f(x₁)＞f(x₂).?

综上讨论,可知n＞0时,f(x)在(0,+∞)上是增函数,n＜0时f(x)在(0,+∞)上是减函数.