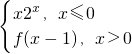题目内容
设函数f（x）满足f（n+1）=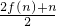
（n∈N*）且f（1）=2，求f（20）的值．
解：∵f（n+1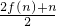）==f（n）+
∴f（n）=f（n-1）+
；
f（n-1）=f（n-2）+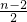
；
…
f（3）=f（2）+1；
f（2）=f（1）+
；
又∵f（1）=2，
∴f（n）=2++1+…+=
∴f（20）=
=97
分析：由已知中函数f（x）满足f（n+1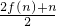）=（n∈N*）且f（1）=2，我们可依次得到f（n）=f（n-1）+；f（n-1）=f（n-2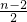）+；…f（2）=f（1）+；结合f（1）=2，利用累加法，我们易求出函数f（n）（n∈N*）的表达式，将n=20代入即可得到f（20）的值．
点评：本题考查的知识点是数列递推式，数列的函数特征，其中由已知条件，结合累加法，得到函数f（n）（n∈N*）的表达式，是解答本题的关键．
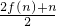=f（n）+∴f（n）=f（n-1）+
；f（n-1）=f（n-2）+
；…
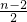f（3）=f（2）+1；
f（2）=f（1）+
；又∵f（1）=2，
∴f（n）=2+
+1+…+=∴f（20）=
=97分析：由已知中函数f（x）满足f（n+1）=
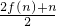（n∈N*）且f（1）=2，我们可依次得到f（n）=f（n-1）+；f（n-1）=f（n-2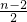）+；…f（2）=f（1）+；结合f（1）=2，利用累加法，我们易求出函数f（n）（n∈N*）的表达式，将n=20代入即可得到f（20）的值．点评：本题考查的知识点是数列递推式，数列的函数特征，其中由已知条件，结合累加法，得到函数f（n）（n∈N*）的表达式，是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知定义在R上的函数f（x）满足：对任意x∈R，都有f（x）=f（2-x）成立，且当x∈（-∞，1）时，（x-1）f′（x）＜0（其中f'（x）为f（x）的导数）．设a=f(0)，b=f(
)，c=f(3)，则a、b、c三者的大小关系是（ ）
| 1 |
| 2 |
| A、a＜b＜c |
| B、c＜a＜b |
| C、c＜b＜a |
| D、b＜c＜a |
设函数f（x）满足f(n+1)=
（n∈N*），且f（1）=2，则f（20）为（ ）
| 2f(n)+n |
| 2 |
| A、95 | B、97 |
| C、105 | D、192 |
