题目内容
如图,已知抛物线C1的方程是y=ax2(a>0),圆C2的方程是x2+(y+1)2=5,直线l:y=2x+m(m<0)是C1,C2的公切线,F是C1的焦点,
(1)求m与a的值;
(2)设A是抛物线C1上的一动点,以A为切点作C1的切线交y轴于点B,若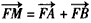 ,则点M在一定直线上,试证明之。
,则点M在一定直线上,试证明之。
(1)求m与a的值;
(2)设A是抛物线C1上的一动点,以A为切点作C1的切线交y轴于点B,若
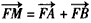 ,则点M在一定直线上,试证明之。
,则点M在一定直线上,试证明之。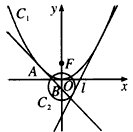
解:(1)由已知,圆C2的圆心为C2(0,-1),半径 ,
,
由题设圆心C2到直线l:y=2x+m(m<0)的距离d= ,
,
解得m=-6(m=4舍去).
设l与抛物线C1相切的切点为A0(x0,y0),
又y′=2ax,得2ax0=2,
所以 ,
,
代入直线方程,得 ,解得
,解得 ,
,
所以m=-6, 。
。
(2)由(1)知抛物线C1的方程为 ,焦点为
,焦点为 ,
,
设 ,
,
由(1)知以A为切点的切线方程为 ,
,
令x=0,得点B的坐标为 ,
,
则
 ,
,
 ,
,
所以 =(x1,-3),
=(x1,-3),
设M(x,y),
则
 =(x1,-3),
=(x1,-3),
所以 ,即M点在定直线
,即M点在定直线 上。
上。
 ,
,由题设圆心C2到直线l:y=2x+m(m<0)的距离d=
 ,
,解得m=-6(m=4舍去).
设l与抛物线C1相切的切点为A0(x0,y0),
又y′=2ax,得2ax0=2,
所以
 ,
,代入直线方程,得
 ,解得
,解得 ,
,所以m=-6,
 。
。(2)由(1)知抛物线C1的方程为
 ,焦点为
,焦点为 ,
,设
 ,
,由(1)知以A为切点的切线方程为
 ,
,令x=0,得点B的坐标为
 ,
,则

 ,
,
 ,
,所以
 =(x1,-3),
=(x1,-3),设M(x,y),
则

 =(x1,-3),
=(x1,-3),所以
 ,即M点在定直线
,即M点在定直线 上。
上。
练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
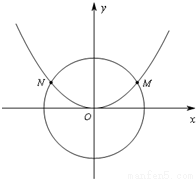
 (2013•嘉兴二模)如图,已知抛物线
(2013•嘉兴二模)如图,已知抛物线 (2013•嘉兴二模)如图,已知抛物线C1:x2=2py的焦点在抛物线C2:
(2013•嘉兴二模)如图,已知抛物线C1:x2=2py的焦点在抛物线C2: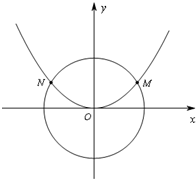 如图,已知抛物线C1:x2=2py(p>0)与圆
如图,已知抛物线C1:x2=2py(p>0)与圆
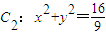 交于M、N两点,
交于M、N两点,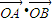 的取值范围.
的取值范围.