题目内容
若实数x、y、m满足|x﹣m|<|y﹣m|,则称x比y接近m.
(1)若2x﹣1比3接近0,求x的取值范围;
(2)对任意两个不相等的正数a、b,证明:a2b+ab2比a3+b3接近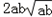 .
.
(1)若2x﹣1比3接近0,求x的取值范围;
(2)对任意两个不相等的正数a、b,证明:a2b+ab2比a3+b3接近
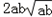 .
.(1)解:若2x﹣1比3接近0,则有|2x﹣1﹣0|<|3﹣0|,
∴|2x﹣1|<3,即﹣3<2x﹣1<3,
解得﹣1<x<2,故x的取值范围为 (﹣1,2).
(2)证明:对任意两个不相等的正数a、b,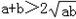 ,
,
有a2b+ab2 >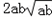 ,
,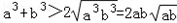 ,即
,即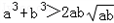 .
.
又因为|a2b+ab2 ﹣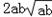 |﹣|
|﹣|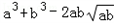 |
|
=ab(a+b)﹣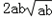 ﹣(a3+b3)+
﹣(a3+b3)+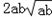
=ab(a+b)﹣(a+b)(a2+b2﹣ab)
=﹣(a+b)(a﹣b)2<0,
所以,|a2b+ab2 ﹣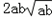 |<|
|<|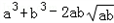 |,
|,
即a2b+ab2比a3+b3接近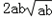 .
.
∴|2x﹣1|<3,即﹣3<2x﹣1<3,
解得﹣1<x<2,故x的取值范围为 (﹣1,2).
(2)证明:对任意两个不相等的正数a、b,
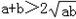 ,
,有a2b+ab2 >
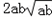 ,
,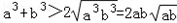 ,即
,即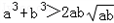 .
.又因为|a2b+ab2 ﹣
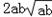 |﹣|
|﹣|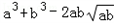 |
|=ab(a+b)﹣
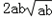 ﹣(a3+b3)+
﹣(a3+b3)+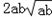
=ab(a+b)﹣(a+b)(a2+b2﹣ab)
=﹣(a+b)(a﹣b)2<0,
所以,|a2b+ab2 ﹣
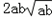 |<|
|<|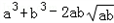 |,
|,即a2b+ab2比a3+b3接近
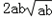 .
.
练习册系列答案
相关题目