题目内容
设直线l:y=k(x+1)(k≠0)与椭圆3x2+y2=a2(a>0)相交于A,B两个不同的点,与x轴相交于点C,记O为坐标原点.
(1)证明:a2>
(2)若k=
且
=2
,求△OAB的面积及椭圆方程.
(1)证明:a2>
| 3k2 |
| 3+k2 |
(2)若k=
| 3 |
| AC |
| CB |
分析:(1)由直线l与椭圆相交于A,B两个不同的点,故联立直线方程和椭圆方程所得方程组有两组根,进而可得方程(
+1)y2-
y+3-a2=0的△>0,化简后可得结论;
(2)设A(x1,y1),B(x2,y2),由
=2
,可得y1=-2y2,由韦达定理可得y1+y2=
,求出y2后,可得△OAB的面积及椭圆方程.
| 3 |
| k2 |
| 6 |
| k |
(2)设A(x1,y1),B(x2,y2),由
| AC |
| CB |
| 3 |
解答:证明:(1)由
得:
(
+1)y2-
y+3-a2=0…①
∵直线l与椭圆相交于A,B两个不同的点,
∴方程①有两个不等的实根,
即△=(
)2-4(
+1)(3-a2)>0
即(
+1)a2>3
即a2>
解:(2)设A(x1,y1),B(x2,y2),
当k=
时,方程①可化为:2y2-2
y+3-a2=0
∴y1+y2=
…②
又∵
=2
,C点坐标为(-1,0)
∴(-1-x1,-y1)=2(x2+1,y2),
即y1=-2y2…③
由②③得:y2=-
,y1=2
∴△OAB的面积S=
•|OC|•|y1-y2|=
将y2=-
,代入2y2-2
y+3-a2=0得:a2=15
故椭圆的方程为:3x2+y2=15
|
(
| 3 |
| k2 |
| 6 |
| k |
∵直线l与椭圆相交于A,B两个不同的点,
∴方程①有两个不等的实根,
即△=(
| 6 |
| k |
| 3 |
| k2 |
即(
| 3 |
| k2 |
即a2>
| 3k2 |
| 3+k2 |
解:(2)设A(x1,y1),B(x2,y2),
当k=
| 3 |
| 3 |
∴y1+y2=
| 3 |
又∵
| AC |
| CB |
∴(-1-x1,-y1)=2(x2+1,y2),
即y1=-2y2…③
由②③得:y2=-
| 3 |
| 3 |
∴△OAB的面积S=
| 1 |
| 2 |
3
| ||
| 2 |
将y2=-
| 3 |
| 3 |
故椭圆的方程为:3x2+y2=15
点评:本题考查的知识点是直线与圆锥曲线,椭圆的标准方程,是高考的压轴题型,运算量大,综合性强,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
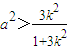 ;
;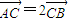 ,△OAB的面积取得最大值时椭圆方程.
,△OAB的面积取得最大值时椭圆方程.