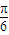题目内容
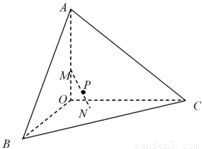
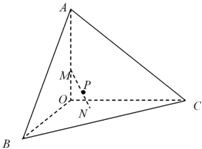 已知三棱锥A-BCO,OA、OB、OC两两垂直且长度均为6,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的面所围成的几何体的体积为
已知三棱锥A-BCO,OA、OB、OC两两垂直且长度均为6,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的面所围成的几何体的体积为
- A.

- B.
 或36+
或36+
- C.36-

- D.
 或36-
或36-
D
分析:由于长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),有空间想象能力可知MN的中点P的轨迹为以O为球心,以1为半径的球体,故MN的中点P的轨迹与三棱锥的面所围成的几何体的体积,利用体积分割及球体的体积公式即可.
解答:因为长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),
有空间想象能力可知MN的中点P的轨迹为以O为球心,以1为半径的球体,则MN的中点P的轨迹与三棱锥的面所围成的几何体可能为该球体的 或该三棱锥减去此球体的
或该三棱锥减去此球体的 ,即:
,即: 或
或 .
.
故选D
点评:此题考查了学生的空间想象能力,还考查了球体,三棱锥的体积公式即计算能力.
分析:由于长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),有空间想象能力可知MN的中点P的轨迹为以O为球心,以1为半径的球体,故MN的中点P的轨迹与三棱锥的面所围成的几何体的体积,利用体积分割及球体的体积公式即可.
解答:因为长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),
有空间想象能力可知MN的中点P的轨迹为以O为球心,以1为半径的球体,则MN的中点P的轨迹与三棱锥的面所围成的几何体可能为该球体的
 或该三棱锥减去此球体的
或该三棱锥减去此球体的 ,即:
,即: 或
或 .
.故选D
点评:此题考查了学生的空间想象能力,还考查了球体,三棱锥的体积公式即计算能力.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
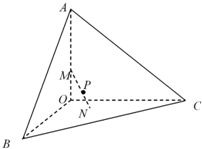 已知三棱锥A-BCO,OA、OB、OC两两垂直且长度均为6,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的面所围成的几何体的体积为( )
已知三棱锥A-BCO,OA、OB、OC两两垂直且长度均为6,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的面所围成的几何体的体积为( )A、
| ||||
B、
| ||||
C、36-
| ||||
D、
|
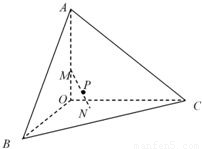
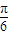
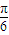 或36+
或36+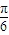
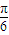
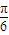 或36-
或36-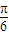
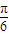
 或36+
或36+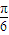

 或36-
或36-
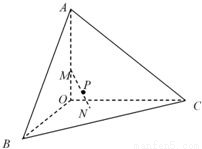
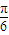
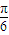 或36+
或36+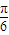
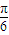
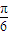 或36-
或36-