题目内容
(本小题满分13分)
设函数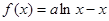 ,其中
,其中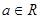 ,且a≠0.
,且a≠0.
(Ⅰ)当a=2时,求函数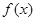 在区间[1,e]上的最小值;
在区间[1,e]上的最小值;
(Ⅱ)求函数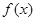 的单调区间。
的单调区间。
设函数
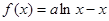 ,其中
,其中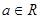 ,且a≠0.
,且a≠0.(Ⅰ)当a=2时,求函数
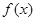 在区间[1,e]上的最小值;
在区间[1,e]上的最小值;(Ⅱ)求函数
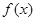 的单调区间。
的单调区间。(Ⅰ)-1(Ⅱ)当a<0时,函数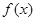 区间(0,+∞)上单调递减,当a>0时,函数
区间(0,+∞)上单调递减,当a>0时,函数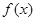 在(0,a)上单调递增,在(a,+∞)上单调递减
在(0,a)上单调递增,在(a,+∞)上单调递减
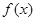 区间(0,+∞)上单调递减,当a>0时,函数
区间(0,+∞)上单调递减,当a>0时,函数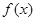 在(0,a)上单调递增,在(a,+∞)上单调递减
在(0,a)上单调递增,在(a,+∞)上单调递减试题分析:(Ⅰ)由题意
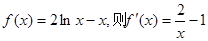 。 1分
。 1分令
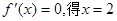 。 2分
。 2分当x变化时,
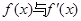 的变化情况如表:
的变化情况如表:| x | 1 | (1,2) | 2 | (2,e) | e |
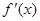 | | + | 0 | - | |
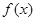 | -1 | ↗ | 极大值 | ↘ | 2-e |
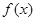 在(1,2)上单调递增,在(2,e)上单调递减。 4分
在(1,2)上单调递增,在(2,e)上单调递减。 4分因为
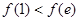 ,
,所以当x=1时,
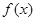 在区间[1,e]上有最小值-1。 5分
在区间[1,e]上有最小值-1。 5分(Ⅱ)函数
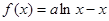 的定义域为(0,+∞)。 6分
的定义域为(0,+∞)。 6分求导,得
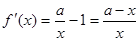 。 7分
。 7分当a<0时,
由x>0,得
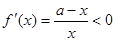 。
。所以
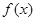 在区间(0,+∞)上单调递减; 9分
在区间(0,+∞)上单调递减; 9分当a>0时,
令
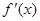 =0,得x=a。 10分
=0,得x=a。 10分当x变化时,
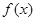 与
与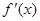 的变化情况如下表:
的变化情况如下表:| x | (0,a) | a | (a,+∞) |
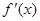 | + | 0 | - |
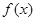 | ↗ | 极大值 | ↘ |
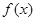 在(0,a)上单调递增,在(a,+∞)上单调递减。
在(0,a)上单调递增,在(a,+∞)上单调递减。综上,当a<0时,函数
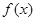 区间(0,+∞)上单调递减;
区间(0,+∞)上单调递减;当a>0时,函数
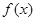 在(0,a)上单调递增,在(a,+∞)上单调递减。 13分
在(0,a)上单调递增,在(a,+∞)上单调递减。 13分点评:函数的最值出现在闭区间的端点处或极值点处,因此只需求出端点处函数值极值后比较大小得最值,在求单调区间时要注意函数的定义域,第二问中因为定义域
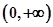 ,因此要对参数a分情况讨论
,因此要对参数a分情况讨论
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
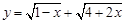 的最大值.
的最大值. ]上是减函数的是
]上是减函数的是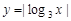 在区间
在区间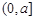 上单调递减,则实数
上单调递减,则实数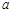 的取值范围为 .
的取值范围为 . 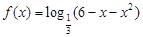 的单调递增区间是
的单调递增区间是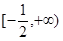
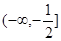
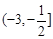
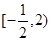
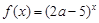 是R上的减函数,命题Q:在
是R上的减函数,命题Q:在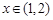 时,不等式
时,不等式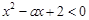 恒成立,若命题“
恒成立,若命题“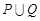 ”是真命题,求实数
”是真命题,求实数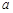 的取值范围.
的取值范围.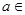 R,函数
R,函数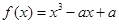 .
.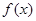 的单调区间;
的单调区间;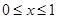 时,
时,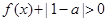 .
.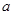 ∈R,函数
∈R,函数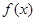 =
=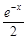 (
(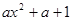 ),其中e是自然对数的底数.
),其中e是自然对数的底数.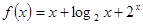 ,则
,则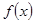 在区间
在区间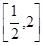 上的值域为
上的值域为