Question

14．已知在△BCE中，D是边BC上一点，满足CD=2BD=2CE=4，P是边BE上一点．满足∠BPD=∠DCE=60°．
（1）求证：P，D，C，E四点共圆，并求其外接圆的面积；
（2）求BP的长．

Answer 1

分析 （1）根据圆内接四边形的判定定理，易证P，D，C，E四点共圆，进而判断出CD为圆的直径，可得外接圆的面积；
（2）利用余弦定理，求出BE，利用切割线定理，可得BP的长．

解答 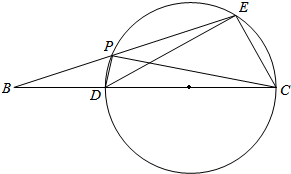证明：（1）如下图所示：
∵∠BPD=∠DCE=60°，
∴P，D，C，E四点共圆，
又∵CD=2BD=2CE=4，
∴DE=$\sqrt{{CD}^{2}+{CE}^{2}-2CD•CE•cos∠DCE}$=$\sqrt{16+4-8}$=2$\sqrt{3}$，
∴CD²=CE²+DE²，即∠DEC=90°，
故CD即为P，D，C，E所在圆的直径，
故圆面积S=4π；
（2）由余弦定理得：BE=$\sqrt{{BC}^{2}+{CE}^{2}-2BC•CE•cos∠DCE}$=$\sqrt{36+4-12}$=2$\sqrt{7}$，
由切割线定理得：BP•BE=BD•BC，即2$\sqrt{7}$BP=12，
∴BP=$\frac{6\sqrt{7}}{7}$

点评 本题考查的知识点是圆内接四边形的判定定理，余弦定理，难度中档．