题目内容
如图，PC与圆O相切于点C，直线PO交圆O于A，B两点，弦CD垂直AB于E．则下面结论中，错误的结论是（ ）分析：利用垂径定理、切割线定理及相似三角形的判定方法即可判断出结论．
解答：解：A．∵∠CEB=∠AED，∠BCE=∠DAE，∴△BEC∽△DEA，因此A正确；
B．∵PC与圆O相切于点C，∴∠PCA=∠B=∠ACE，因此B正确；
C．连接OC，则OC⊥PC，又CD⊥AB，∴CE2=OE•EP，CE=ED，∴ED2=OE•EP，因此C正确；
D．由切割线定理可知：PC2=PA•PB≠PA•AB，因此D不正确．
故选D．
B．∵PC与圆O相切于点C，∴∠PCA=∠B=∠ACE，因此B正确；
C．连接OC，则OC⊥PC，又CD⊥AB，∴CE2=OE•EP，CE=ED，∴ED2=OE•EP，因此C正确；
D．由切割线定理可知：PC2=PA•PB≠PA•AB，因此D不正确．
故选D．
点评：熟练掌握垂径定理、切割线定理及相似三角形的判定方法是解题的关键．
练习册系列答案
轻松暑假总复习系列答案
相关题目
如图，PA与圆O相切于A，PCB为圆O的割线，并且不过圆心O，已知∠BPA=30°，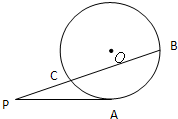
A．（极坐标系与参数方程选做题） 已知圆ρ=3cosθ，则圆截直线
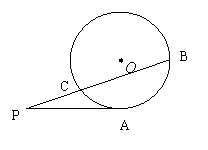PCB为圆O的割线，并且不过圆心O，已知
∠BPA=
，
，PC=1，则圆O的半径等于 ．
如图，PC与圆O相切于点C，直线PO交圆O于A，B两点，弦CD垂直AB于E．则下面结论中，错误的结论是