Question

正三棱柱ABC—A₁B₁C₁的底面边长为a,在侧棱BB₁上截取BD=,在侧棱CC₁上截取CE=a,过A,D,E作棱柱的截面.求证:截面ADE⊥侧面ACC₁A₁.

Answer 1

证明：取BC的中点O,如图建立空间直角坐标系.

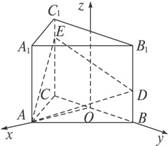
则A(a,0,0),B(0,a2,0),D(0,,),E(0,-,a),C(0,-,0).

所以=(-a,,),=(-a,-,a).

设平面ADE的法向量为n₁=(x₁,y₁,z₁),则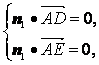

所以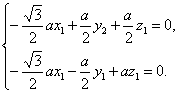

令y₁=1,则n₁=(,1,2).

又=(-a,,0).

设平面ACC₁A₁的法向量为n₂=(x₂,y₂,z₂).

所以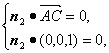

所以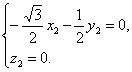

令x₂=1,则n₂=(1,,0).

所以n₁·n₂=0.所以n₁⊥n₂.

所以截面ADE⊥侧面ACC₁A₁.