题目内容
数列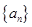 的前
的前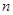 项和记为
项和记为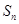 ,
,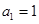 ,
,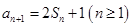 .
.
(1)求数列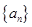 的通项公式;
的通项公式;
(2)等差数列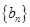 的前
的前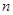 项和
项和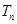 有最大值,且
有最大值,且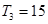 ,又
,又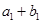 、
、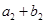 、
、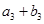 成等比数列,求
成等比数列,求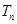 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)将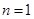 代入式子
代入式子 结合
结合 求出
求出 的值,然后令
的值,然后令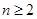 ,由
,由 得到
得到 ,两式相减并化简得
,两式相减并化简得 ,需注意这个等式是在
,需注意这个等式是在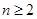 的前提下成立,因此要对
的前提下成立,因此要对 与
与 之间是否满足这个等式进行检验,否则数列
之间是否满足这个等式进行检验,否则数列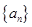 从第二项开始才成等比数列,从而确定数列
从第二项开始才成等比数列,从而确定数列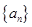 的通项公式;(2)根据等差数列
的通项公式;(2)根据等差数列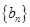 的前
的前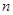 项和有最大值得到该数列的公差为负,然后根据后面两个条件求出等差数列
项和有最大值得到该数列的公差为负,然后根据后面两个条件求出等差数列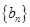 的首项和公差,从而确定等差数列
的首项和公差,从而确定等差数列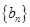 的通项公式,进而求出等差数列
的通项公式,进而求出等差数列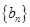 的前
的前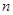 项和
项和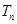 .
.
试题解析:(1)由 ,可得
,可得 ,
,
两式相减得 ,
, ,
,
又 ,
, ,
,
故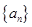 是首项为
是首项为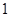 ,公比为
,公比为 的等比数列,
的等比数列, ;
;
(2)设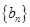 的公差为
的公差为 ,
,
由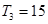 得
得 ,于是
,于是 ,
,
故可设 ,
, ,
,
又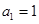 ,
, ,
, ,
,
由题意可得 ,
,
解得 ,
, ,
,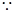 等差数列
等差数列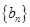 的前
的前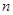 项和
项和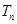 有最大值,
有最大值, ,
, ,
, .
.
考点:1.定义法求数列通项;2.等差数列中基本量的应用;3.等差数列求和

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 中,前n项和为
中,前n项和为 ,且
,且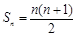 .
.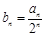 ,数列
,数列 前n项和为
前n项和为 ,比较
,比较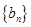 是首项为1,公差为2的等差数列,数列
是首项为1,公差为2的等差数列,数列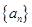 的前n项和
的前n项和 .
. , 求数列
, 求数列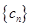 的前n项和
的前n项和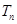 .
. 、
、 满足
满足 ,且
,且 ,其中
,其中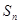 为数列
为数列 项和,又
项和,又 ,对任意
,对任意 都成立。
都成立。 的前
的前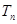
 中,
中,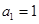 ,
, ,数列
,数列 中,
中,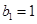 ,且点
,且点 在直线
在直线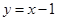 上.
上.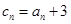 ,求数列
,求数列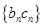 的前项和
的前项和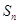 .
.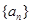 是公比大于1的等比数列,
是公比大于1的等比数列,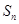 为数列
为数列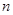 项和.已知
项和.已知 ,且
,且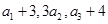 构成等差数列.
构成等差数列.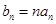 ,求数列
,求数列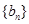 的前
的前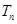 .
. 的方程为
的方程为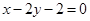 ,数列
,数列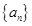 满足
满足 ,其前
,其前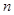 项和为
项和为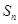 ,点
,点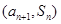 在直线
在直线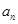 和
和 之间插入
之间插入 个数组成公差为
个数组成公差为 的等差数列,令
的等差数列,令 ,试证明
,试证明 .
. 为等差数列
为等差数列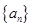 的前
的前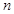 项和,且
项和,且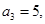
 .
.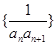 的前
的前 .
.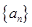 是各项都为正数的等比数列,
是各项都为正数的等比数列,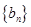 是等差数列,且
是等差数列,且 ,
,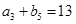 ,
,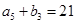 .
.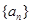 ,
,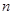 项和为
项和为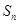 ,求数列
,求数列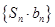 的前
的前 .
.