题目内容
已知函数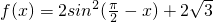 sin(π-x)cosx,
sin(π-x)cosx,
(1)求函数f(x)在 上的值域;
上的值域;
(2)在△ABC中,若f(C)=2,2sinB=cos(A-C)-cos(A+C),求tanA.
解:化简函数为:f(x)=2cos2x+2 ,
,
(1)当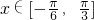 时,2x+
时,2x+ ,
,
∴ ,2sin(2x)+1∈[0,3],即f(x)∈[0,3];
,2sin(2x)+1∈[0,3],即f(x)∈[0,3];
∴函数f(x)的值域为[0,3].
(2)由条件知 ,
,
即: ,0<C<π,所以C=
,0<C<π,所以C= ,
,
又∵2sinB=cos(A-C)-cos(A+C),
∴2sinB=cosAcosC+sinAsinC-(cosAcosC-sinAsinC),
∴sinB=sinAsinC,由C= ,A+B+C=π可得:
,A+B+C=π可得:
sin(A+C)= sinA,即sinAcosC+cosAsinC=
sinA,即sinAcosC+cosAsinC= sinA,
sinA,
所以: tanA,
tanA,
解得:tanA=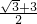 .
.
分析:(1)利用三角函数的降幂公式与倍角公式,辅助角公式将函数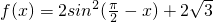 sin(π-x)cosx转化为:
sin(π-x)cosx转化为:
y=2sin(2x+ ),由x∈
),由x∈ ?2x+
?2x+ ,由正弦函数的图象与性质可求得函数f(x)在
,由正弦函数的图象与性质可求得函数f(x)在 上的值域;
上的值域;
(2)由 ,0<C<π?C=
,0<C<π?C= ;2sinB=cos(A-C)-cos(A+C)?sinB=sinAsinC
;2sinB=cos(A-C)-cos(A+C)?sinB=sinAsinC
?sin(A+C)=sinAsinC,展开整理即可求得tanA.
点评:本题考查复合三角函数的单调性,(1)中难点在于由x∈ ?2x+
?2x+ ,再利用正弦函数的图象与性质予以解决,(2)着重考查三角函数的恒等变换及化简求值,属于中档题.
,再利用正弦函数的图象与性质予以解决,(2)着重考查三角函数的恒等变换及化简求值,属于中档题.
 ,
,(1)当
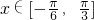 时,2x+
时,2x+ ,
,∴
 ,2sin(2x)+1∈[0,3],即f(x)∈[0,3];
,2sin(2x)+1∈[0,3],即f(x)∈[0,3];∴函数f(x)的值域为[0,3].
(2)由条件知
 ,
,即:
 ,0<C<π,所以C=
,0<C<π,所以C= ,
,又∵2sinB=cos(A-C)-cos(A+C),
∴2sinB=cosAcosC+sinAsinC-(cosAcosC-sinAsinC),
∴sinB=sinAsinC,由C=
 ,A+B+C=π可得:
,A+B+C=π可得:sin(A+C)=
 sinA,即sinAcosC+cosAsinC=
sinA,即sinAcosC+cosAsinC= sinA,
sinA,所以:
 tanA,
tanA,解得:tanA=
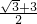 .
.分析:(1)利用三角函数的降幂公式与倍角公式,辅助角公式将函数
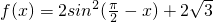 sin(π-x)cosx转化为:
sin(π-x)cosx转化为:y=2sin(2x+
 ),由x∈
),由x∈ ?2x+
?2x+ ,由正弦函数的图象与性质可求得函数f(x)在
,由正弦函数的图象与性质可求得函数f(x)在 上的值域;
上的值域;(2)由
 ,0<C<π?C=
,0<C<π?C= ;2sinB=cos(A-C)-cos(A+C)?sinB=sinAsinC
;2sinB=cos(A-C)-cos(A+C)?sinB=sinAsinC?sin(A+C)=sinAsinC,展开整理即可求得tanA.
点评:本题考查复合三角函数的单调性,(1)中难点在于由x∈
 ?2x+
?2x+ ,再利用正弦函数的图象与性质予以解决,(2)着重考查三角函数的恒等变换及化简求值,属于中档题.
,再利用正弦函数的图象与性质予以解决,(2)着重考查三角函数的恒等变换及化简求值,属于中档题. 
练习册系列答案
相关题目
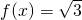 sin(ωx-
sin(ωx- .
. )的值;
)的值;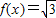 sin(ωx-
sin(ωx- )-cos(ωx-
)-cos(ωx- )(ω>0)图象的两相邻对称轴间的距离为
)(ω>0)图象的两相邻对称轴间的距离为 .
. )的值;
)的值; 个单位后,得到函数y=g(x)图象,求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求g(x)在区间[0, ]上的单调性.
]上的单调性.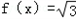 sin(
sin(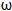 x﹣
x﹣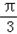 )﹣cos(
)﹣cos(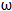 x﹣
x﹣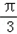 )(
)(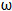 >0)图象的两相邻对称轴间的距离为
>0)图象的两相邻对称轴间的距离为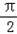 .
. 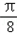 )的值;
)的值;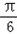 个单位后,得到函数y=g(x)图象,求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求g(x)在区间[0,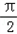 ]上的单调性.
]上的单调性.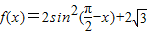 sin(π-x)cosx,
sin(π-x)cosx,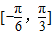 上的值域;
上的值域;