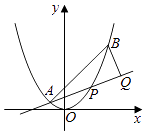
[题目]在平面直角坐标系中.已知椭圆的离心率为.两个顶点分别为.．过点的直线交椭圆于.两点.直线与的交点为．(1)求椭圆的标准方程, (2)求证:点在一条定直线上．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】在平面直角坐标系中，已知椭圆的离心率为，两个顶点分别为，．过点的直线交椭圆于，两点，直线与的交点为．

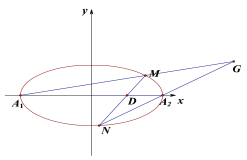
(1)求椭圆的标准方程；

(2)求证：点在一条定直线上．

【答案】（1）；（2）见解析

【解析】

（1）由已知得a=2．e==，由此能求出a，b；

（2）设直线A1M的方程为y=k1（x+2），直线A2N的方程为y=k2（x﹣2）．联立方程组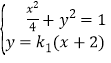，得点M的坐标为（，），同理，点N（，）．由M，D，N三点共线，得k2=3k1，由此能证明点G恒在定直线x=4上．

(1)由椭圆两个顶点分别为，题设可知

因为，即，所以．

又因为，所以．

所以，所求的椭圆的标准方程为.

(2)由题意知，直线与直线的斜率存在，故设直线的方程为，直线的方程为．

联立方程组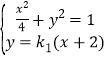，消去y得，

解得点．同理，解得点.

由M，D，N三点共线，有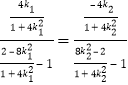，化简得．

由题设可知与同号，所以．

联立方程组，解得交点．将代入点G的横坐标，

得．所以，点G恒在定直线上．

练习册系列答案

相关题目

【题目】如图，已知抛物线x2=y，点A（﹣ ，），B（，），抛物线上的点P（x，y）（﹣ ＜x＜），过点B作直线AP的垂线，垂足为Q．
（Ⅰ）求直线AP斜率的取值范围；
（Ⅱ）求|PA||PQ|的最大值．

【题目】已知函数f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，且导函数f′（x）的极值点是f（x）的零点．（极值点是指函数取极值时对应的自变量的值）
（Ⅰ）求b关于a的函数关系式，并写出定义域；
（Ⅱ）证明：b2＞3a；
（Ⅲ）若f（x），f′（x）这两个函数的所有极值之和不小于﹣ ，求a的取值范围．

【题目】设O为坐标原点，动点M在椭圆C： +y2=1上，过M做x轴的垂线，垂足为N，点P满足 = ．
（Ⅰ）求点P的轨迹方程；
（Ⅱ）设点Q在直线x=﹣3上，且 =1．证明：过点P且垂直于OQ的直线l过C的左焦点F．

【题目】在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρcosθ=4．
（Ⅰ）M为曲线C1上的动点，点P在线段OM上，且满足|OM||OP|=16，求点P的轨迹C2的直角坐标方程；
（Ⅱ）设点A的极坐标为（2，），点B在曲线C2上，求△OAB面积的最大值．

【题目】已知曲线C1：y=cosx，C2：y=sin（2x+ ），则下面结论正确的是（　　）
A.把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2
C.把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2
D.把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2