题目内容
求证:两条平行线段之比等于它们的平行射影之比.
证明:如图
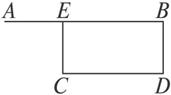
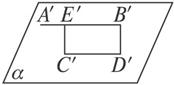
图
假设A′B′与C′D′不平行而它们的延长线相交于点P′,且设其为P的平行射影.那么P既在直线AB上又在直线CD上(否则过P′点就会有两条直线与投影方向平行),即AB、CD不平行,与题设矛盾.
∴A′B′∥C′D′.
分别过C作CE∥DB交AB于E,过C′作C′E′∥D′B′交A′B′于E′,
则BE=CD,C′D′=B′E′,且E′是E在α上的平行射影.
这样,![]() ,∴
,∴![]() =
=![]() .
.

练习册系列答案
相关题目