题目内容

（2006•广州一模）已知向量
a
=(2，3)，|
b
|=2
13
，且
a
∥
b
，则向量
b
的坐标为（　　）
分析：设出向量
b
的坐标，然后根据条件列出方程组，解方程组即可
解答：解：设
b
=(m，n)
∵|
b
|=2
13

∴
m2+n2
=2
13
，即m2+n2=52
又
a
∥
b
，且
a
=(2，3)
∴3m-2n=0
联立方程组
m2+n2=52
3m-2n=0

解得：m=4，n=6或m=-4，n=-6
即向量
b
的坐标为（4，6）或（-4，-6）
故选D
点评：本题考查向量平行的坐标条件和向量的模的运算．属简单题
练习册系列答案
相关题目
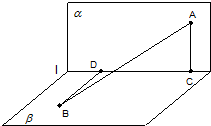（2006•广州一模）如图，长度为2的线段AB夹在直二面角α-l-β的两个半平面内，A∈α，B∈β，
且AB与平面α、β所成的角都是30°，AC⊥l，垂足为C，BD⊥l，垂足为D．
（Ⅰ）求直线AB与CD所成角的大小；
（Ⅱ）求二面角C-AB-D所成平面角的余弦值．
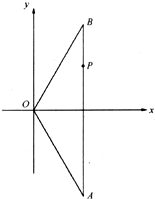（2006•广州一模）如下图，在△OAB中，|OA|=|OB|=4，点P分线段AB所成的比为3：1，以OA、OB所在直线为渐近线的双曲线M恰好经过点P，且离心率为2．
（1）求双曲线M的标准方程；
（2）若直线y=kx+m（k≠0，m≠0）与双曲线M交于不同的两点E、F，且E、F两点都在以Q（0，-3）为圆心的同一圆上，求实数m的取值范围．
（2006•广州一模）函数y=f（x）是定义在R上的增函数，y=f（x）的图象经过点（0，-1）和下面下面的哪一个点时，能使不等式-1＜f（x+1）＜1的解集为{x|-1＜x＜3}（　　）
（2006•广州一模）已知sin
α
2
-cos
α
2
=
5
5
，α∈(
π
2
，π)，tanβ=
1
2
．
（Ⅰ）求sinα的值；
（Ⅱ）求tan（α-β）的值．
（2006•广州一模）记等差数列{an}的前n项和为Sn，若a9=10，则 S17=
170
170
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网