题目内容
（本小题满分12分）
已知
求g(x)=
的单调区间；
证明：当x
1时，2x-e
恒成立；
任取两个不相等的正数
且
<
若存在
使
成立，证明：
。
解：(1)g(x)=lnx+
得x=k 
——2分
时
所以函数g(x)的增区间为
，无减区间；
当k>0时得x>k ; 
得0<x<k
增区间为
, 减区间为(0,k)————————————4分
(2)设h(x)=xlnx-2x+e(x
1)令
得x=e
所以
| x | 1 | (1,e) | e | (e,+ |
|
| - | 0 | + | |
| h(x) | e-2 |
| 0 |
|
)
所以h(x)0 f(x)2x-e——————————-————6分
设G(x)=lnx-
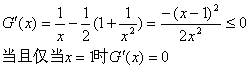
所以G(x)为增函数，所以G(x)
所以lnx-
所以
综上：当x1时，2x-e
恒成立———————8分
(3)
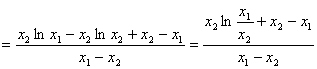
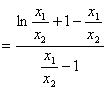——10分
设H(t)=lnt+1-t(0<t<1) 
所以H(t)在（0，1）上是增函数，并且H(t)在t=1处有意义
所以H(t)<H(1)=0
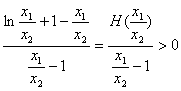
——12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
