题目内容
已知无穷等比数列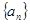 的前
的前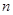 项和
项和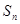 的极限存在,且
的极限存在,且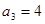 ,
,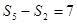 ,则数列
,则数列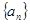 各项的和为______________.
各项的和为______________.
【答案】

【解析】
试题分析:根据题意可得 ,可解得
,可解得 ,因为
,因为 存在极限,则
存在极限,则 ,再由等比数列求和公式可得
,再由等比数列求和公式可得 .
.
考点:1.等比数列的基本量运算;2.数列的极限

练习册系列答案
相关题目
已知无穷等比数列{an}的前n项和Sn=
+a(n∈N*),且a是常数,则此无穷等比数列各项的和是( )
| 1 |
| 3n |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
(2007
成都模拟)已知无穷等比数列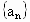 的公比为
的公比为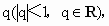
 为其前n项和
为其前n项和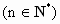 ,又
,又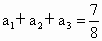 ,
,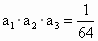 ,则
,则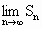 的值为
的值为
[
]|
A .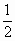 |
B .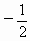 |
C .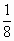 |
D .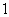 |